
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB; 
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF. 
【答案】
(1)连接OC,
∵直线l与⊙O相切于点C,
∴OC⊥CD;
又∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠ACO;
又∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB;
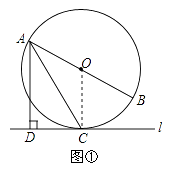
(2)如图②,连接BF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠BAF=90°﹣∠B,
∴∠AEF=∠ADE+∠DAE,
在⊙O中,四边形ABFE是圆的内接四边形,
∴∠AEF+∠B=180°,
∴∠BAF=∠DAE.

【解析】(1)连接OC,易得OC∥AD,根据平行线的性质就可以得到∠DAC=∠ACO,再根据OA=OC得到∠ACO=∠CAO,就可以证出结论;(2)如图②,连接BF,由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠AFB=90°,由三角形外角的性质,可求得∠AEF的度数,又由圆的内接四边形的性质,继而证得结论.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A点的坐标为(0,4),B点的坐标为(3,0),C(a,b)为平面直角坐标系内一点,若∠ABC=90°,且BA=BC,求ab的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
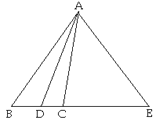
【题目】如图,AD平分∠BAC,∠EAD=∠EDA.
(1)∠EAC与∠B相等吗?为什么?
(2)若∠B=50°,∠CAD︰∠E=1︰3,求∠E的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1、2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△OAB中,∠AOB=90°,已知AB= ![]() ,AO:BO=1:3,将△OAB绕点O按顺时针方向旋转90°得到△ODC,如图1建立平面直角坐标系.
,AO:BO=1:3,将△OAB绕点O按顺时针方向旋转90°得到△ODC,如图1建立平面直角坐标系.
(1)求A,B,C三点坐标;
(2)若抛物线y=ax2+bx+c(a≠0)经过A,B,C三点(如图2),点P是抛物线的顶点,试判定△PCD的形状,并说明理由:
(3)在(2)的抛物线上,且在第一象限中,是否存在点Q,使S△QCD=S△OCD?若存在,请求点Q的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( ) 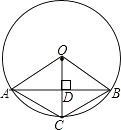
A.AD=BD
B.OD=CD
C.∠CAD=∠CBD
D.∠OCA=∠OCB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)解方程:x2=2x.
(2)如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC向右平移至△A′B′C′的位置,使得四边形ABB′A′为菱形,求B′C的长. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com