
【题目】某公司有火车车皮和货车可供租用,货主准备租用火车车皮和货车运输一批物资,已知以往用这种火车车皮和货车运货情况如下表:
第一次 | 第二次 | |
火车车皮(节) | 6 | 8 |
货车(辆) | 15 | 10 |
累计运货(吨) | 360 | 440 |
(1)每节火车车皮和每辆货车平均各装物资多少吨?
(2)若货主需要租用该公司的火车车皮7节,货车10辆,刚好运完这批货物,如按每吨付运费60元,则货主应付运费总额为多少元?
(3)若货主共有300吨货,计划租用该公司的火车车皮或货车正好(每节车皮和每辆货车都满载)把这批货运完,该公司共有哪几种运货方案?写出所有的方案.
【答案】(1)每节火车车皮和每辆货车平均各装物资50吨,4吨.(2)货主应付运费总额为23400元.(3)该公司共有4种运货方案:租6节火车车皮,0辆货车;租4节火车车皮,25辆货车;租2节火车车皮,50辆货车;租0节火车车皮,75辆货车.
【解析】
(1)设每节火车车皮和每辆货车平均各装物资x吨,y吨,根据表格中提供的数据列出方程组解答即可;
(2)直接代入求得答案即可;
(3)设租a节火车车皮,b辆货车,根据(1)求得的结果可列二元一次方程,然后在讨论其非负整数解即可.
(1)设每节火车车皮和每辆货车平均各装物资x吨,y吨,由题意得
![]()
解得![]()
答:每节火车车皮和每辆货车平均各装物资50吨,4吨.
(2)7×50×60+10×4×60
=21000+2400
23400(元).
答:货主应付运费总额为23400元.
(3)设租a节火车车皮,b辆货车,正好(每节车皮和每辆货车都满载)把这批货运完,
50a+4b=300,
则b=![]() ,
,
∵a、b都是非负整数,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
答:该公司共有4种运货方案:租6节火车车皮,0辆货车;租4节火车车皮,25辆货车;租2节火车车皮,50辆货车;租0节火车车皮,75辆货车.


科目:初中数学 来源: 题型:
【题目】某商场第1次用39万元购进A、B两种商品,销售完后获得利润6万元,它们的进价和售价如下表:![]() 总利润
总利润![]() 单件利润
单件利润![]() 销售量
销售量![]()
商品价格 | A | B |
进价 | 1200 | 1000 |
售价 | 1350 | 1200 |
(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原进价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原售价销售,而B商品按原售价打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于54000元,则B种商品是打几折销售的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P(x,y)的坐标满足方程组![]()
(1)求点P的坐标(用含m,n的式子表示);
(2)若点P在第四象限,且符合要求的整数m只有两个,求n的取值范围;
(3)若点P到x轴的距离为5,到y轴的距离为4,求m,n的值(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式;
(3)y轴上是否存在一点P,使得S△PAB=![]() ,若存在,请求出点P的坐标;若不存在,请说明理由.
,若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为a、b、c,则这个三角形的面积为![]() ,其中
,其中![]() .这个公式称为“海伦公式”.
.这个公式称为“海伦公式”.
数学应用:
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)请运用海伦公式求△ABC的面积;
(2)设AB边上的高为![]() ,AC边上的高
,AC边上的高![]() ,求
,求![]() 的值;
的值;
(3)如图2,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图,并且C的对应点C′的坐标为(4,1)。
(1)A′、B′.两点的坐标分别为A′ 、B′ ;
(2)请作出△ABC平移之后的图形△A′B′C′;
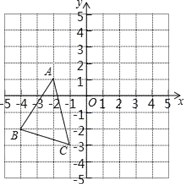
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥BC,垂足为C,AC=2cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_____秒时,△BCA与点P、N、B为顶点的三角形全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com