
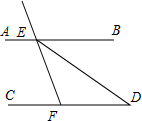
 如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.
如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由. 科目:初中数学 来源: 题型:解答题
 如图,某渔船在A处观测到灯塔M在它的北偏东48°方向上,这艘渔船以每小时28海里的速度向正东方向航行,半小时后到达B处,在B处观测到灯塔M在它的北偏东37°方向上.这艘渔船继续向正东航行多少海里,距离灯塔M最近?(参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin48°≈$\frac{7}{10}$,tan48°≈$\frac{11}{10}$,cos37°≈$\frac{4}{5}$,cos48°≈$\frac{7}{11}$)
如图,某渔船在A处观测到灯塔M在它的北偏东48°方向上,这艘渔船以每小时28海里的速度向正东方向航行,半小时后到达B处,在B处观测到灯塔M在它的北偏东37°方向上.这艘渔船继续向正东航行多少海里,距离灯塔M最近?(参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin48°≈$\frac{7}{10}$,tan48°≈$\frac{11}{10}$,cos37°≈$\frac{4}{5}$,cos48°≈$\frac{7}{11}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
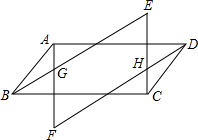 如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点,交BE于E点.
如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点,交BE于E点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-$\frac{1}{5}$<b-$\frac{1}{5}$ | B. | -4a>-4b | C. | -2a+1<-2b+1 | D. | a2>b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数x(cm) | 175 | 173 | 175 | 174 |
| 方差S2(cm2) | 3.5 | 3.5 | 12.5 | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com