
分析 此题分两种情况:当B点落在AD上或落在AD的延长线上,首先根据勾股定理求得AC,然后利用相似三角形的判定与性质得出比例式即可求出结论.
解答 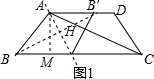 解:如图1所示:∵AB=CD=5,
解:如图1所示:∵AB=CD=5,
由折叠的性质得:AB′=AB=5,
∵DB′=1,
∴AD=6,
过A作AM⊥BC于M,
∵BC=12,AD=6,
∴BM=$\frac{1}{2}$(BC-AD)=3,
∴CM=9,AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=4,
∴AC=$\sqrt{A{M}^{2}+C{M}^{2}}$=$\sqrt{97}$,
∵AD∥BC,
∴△AB′H∽△BCH,
∴$\frac{AH}{CH}=\frac{AB′}{BC}$=$\frac{5}{12}$,
∴$\frac{AH}{AC}$=$\frac{5}{17}$,
∴AH=$\frac{5\sqrt{97}}{17}$;
如图2所示: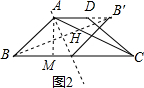 ∵AB=CD=5,
∵AB=CD=5,
由折叠的性质得:AB′=AB=5,
∵DB′=1,
∴AD=4,
过A作AM⊥BC于M,
∵BC=12,AD=4,
∴BM=$\frac{1}{2}$(BC-AD)=4,
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=3,
∴AC=$\sqrt{A{M}^{2}+C{M}^{2}}$=$\sqrt{73}$,
∵AD∥BC,
∴△AB′H∽△BCH,
∴$\frac{AH}{CH}=\frac{AB′}{BC}$=$\frac{5}{12}$,
∴$\frac{AH}{AC}$=$\frac{5}{17}$,
∴AH=$\frac{5\sqrt{73}}{17}$.
故答案为:$\frac{5\sqrt{97}}{17}$,$\frac{5\sqrt{73}}{17}$.
点评 此题主要考查了相似三角形的判定与性质,等腰梯形的性质,勾股定理,利用相似三角形对应边之间的关系得出AH是解题关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 南京 | 常州 | 苏州 | 上海 | |
| 到站时间 | 14:14 | 15:04 | 15:47 | |
| 发车时间 | 13:00 | 14:18 | 15:08 | |
| 里程/km | 0 | 138 | 219 | 303 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2+2 | B. | a+2 | C. | $\sqrt{a+2}$ | D. | $\sqrt{{a^2}+2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com