
| A. | 2 | B. | $\sqrt{5}$+1 | C. | 2或$\sqrt{5}$+1 | D. | 以上都不对 |
分析 先分类讨论:根据黄金分割的定义当AP为较长线段时AP=$\frac{\sqrt{5}-1}{2}$AB,所以AB=$\frac{2}{\sqrt{5}-1}$•AP;当AP为较短线段时,AP=AB-$\frac{\sqrt{5}-1}{2}$AB=$\frac{3-\sqrt{5}}{2}$AB,所以AB=$\frac{2}{3-\sqrt{5}}$AP,然后把AP的长代入计算即可.
解答 解:∵点P是线段AB的黄金分割点,
当AP为较长线段时,AP=$\frac{\sqrt{5}-1}{2}$AB,所以AB=$\frac{2}{\sqrt{5}-1}$•($\sqrt{5}$-1)=2,
当AP为较短线段时,AP=AB-$\frac{\sqrt{5}-1}{2}$AB=$\frac{3-\sqrt{5}}{2}$AB,所以AB=$\frac{2}{3-\sqrt{5}}$•($\sqrt{5}$-1)=$\sqrt{5}$+1,
综上所述,AB的长为2或$\sqrt{5}$+1;
故选C.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:选择题
 如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段8cm,若AP=$\frac{1}{2}$PB,则这条绳子的原长为( )cm.
如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段8cm,若AP=$\frac{1}{2}$PB,则这条绳子的原长为( )cm.| A. | 12 | B. | 24 | C. | 20 或24 | D. | 12或24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 △ABC中,∠C=90°,D是AC边上一点,且CD=CB,AD=BD,则tanA的值是( )
△ABC中,∠C=90°,D是AC边上一点,且CD=CB,AD=BD,则tanA的值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{2}}{2}$ | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
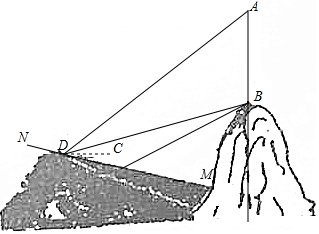 如图所示.在山顶上有一座电视塔AB(AB与水平面垂直),小明同学要测量电视塔AB的高度,在斜坡MN上取一点C,测得塔底B的仰角为30°,坡底M的俯角为15°,小明沿斜坡MN上行20米到点D,在点D测得塔底B的仰角为15°,塔顶A的仰角为45°,请根据以上数据帮助小明求出电视塔AB的高度(结果保留根号).
如图所示.在山顶上有一座电视塔AB(AB与水平面垂直),小明同学要测量电视塔AB的高度,在斜坡MN上取一点C,测得塔底B的仰角为30°,坡底M的俯角为15°,小明沿斜坡MN上行20米到点D,在点D测得塔底B的仰角为15°,塔顶A的仰角为45°,请根据以上数据帮助小明求出电视塔AB的高度(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
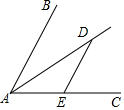 如图,∠BAC=60°,AD是∠BAC的角平分线,点D在AD上,过点D作DE∥AB交AC于点E.若DE=2,则点D到AB的距离为( )
如图,∠BAC=60°,AD是∠BAC的角平分线,点D在AD上,过点D作DE∥AB交AC于点E.若DE=2,则点D到AB的距离为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com