
 的图象与x轴和y轴分别交于点A(6,0)和B(0,
的图象与x轴和y轴分别交于点A(6,0)和B(0, ),线段AB的垂直平分线交x轴于点C,交AB于点D.
),线段AB的垂直平分线交x轴于点C,交AB于点D.
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源:不详 题型:解答题
 与它的对称轴相交于点
与它的对称轴相交于点 ,与
,与 轴交于
轴交于 ,与
,与 轴正半轴交于
轴正半轴交于 .
. 交
交 轴于
轴于 是线段
是线段 上一动点(
上一动点( 点异于
点异于 ),过
),过 作
作 轴交直线
轴交直线 于
于 ,过
,过 作
作 轴于
轴于 ,求当四边形
,求当四边形 的面积等于
的面积等于 时点
时点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,对称轴为
,对称轴为 轴.一次函数
轴.一次函数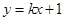 的图象与二次函数的图象交于
的图象与二次函数的图象交于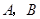 两点(
两点( 在
在 的左侧),且
的左侧),且 点坐标为
点坐标为 .平行于
.平行于 轴的直线
轴的直线 过
过 点.
点.
 为直径的圆与直线
为直径的圆与直线 的位置关系,并给出证明;
的位置关系,并给出证明; 个单位,再向下平移
个单位,再向下平移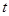 个单位
个单位 ,二次函数的图象与
,二次函数的图象与 轴交于
轴交于 两点,一次函数图象交
两点,一次函数图象交 轴于
轴于 点.当
点.当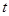 为何值时,过
为何值时,过 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 、
、 ,-1,0、1、3的6张卡片,背面完全相同,洗匀后,从中任取两张,该卡片上的数分别作为点P 的横坐标和纵坐标,P落在抛物线
,-1,0、1、3的6张卡片,背面完全相同,洗匀后,从中任取两张,该卡片上的数分别作为点P 的横坐标和纵坐标,P落在抛物线 与对称轴右侧所围成的区域内(不含边界)的概率是 。
与对称轴右侧所围成的区域内(不含边界)的概率是 。查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
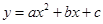 图象的一部分,图象过
图象的一部分,图象过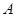 点(3,0),二次函数图象对称轴为
点(3,0),二次函数图象对称轴为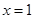 ,给出四个结论:①
,给出四个结论:①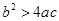 ;②
;②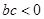 ;③
;③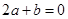 ;④
;④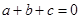 ,其中正确结论是( )
,其中正确结论是( )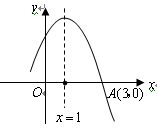
| A.②④ | B.①③ | C.②③ | D.①④ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
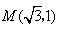 出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长
出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长 ;过点O且垂直于射线OM的直线
;过点O且垂直于射线OM的直线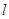 与点P同时出发,且与点P沿相同的方向、以相同的速度运动.
与点P同时出发,且与点P沿相同的方向、以相同的速度运动. 运动过程中,试判断AB与y轴的位置关系,并说明理由.
运动过程中,试判断AB与y轴的位置关系,并说明理由. 与直线L都运动了t秒,求此时的矩形OAPB与直线
与直线L都运动了t秒,求此时的矩形OAPB与直线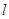 在运动过程中所扫过的区域的重叠部分的面积S(用含t的代数式表示).
在运动过程中所扫过的区域的重叠部分的面积S(用含t的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com