解:(1)∵∠AOC是直角,
∴∠AOC=90°;
又∵∠AOD+∠COD=∠AOC,∠DOC=36°,
∴∠AOD=54°;
∵∠BOD是直角,
∴∠BOD=90°,
∴∠AOB=∠AOD+∠BOD=144°;
(2)∵∠AOB=130°,∠AOC=90°,∠AOC+∠BOC=∠AOB,
∴∠BOC=40°;
又∵∠DOB=90°,∠DOC+∠BOC=∠DOB,
∴∠DOC=50°;
(3)∠DOC<∠AOB.
理由:∵根据图示知,∠DOC=90°-∠BOC,∠AOB=90°+∠BOC,
∴∠AOB-∠DOC=2∠BOC>0,
∴∠DOC<∠AOB.
分析:(1)根据直角的定义可以求得∠AOD=∠AOC-∠DOC;然后由角间的和差关系可以求得∠AOB的度数;
(2)根据图示知∠AOC+∠BOC=∠AOB,据此可以求得∠BOC的度数,然后由直角的定义即可求得∠DOC的度数;
(3)根据图示直接回答问题.
点评:本题考查了角的计算.解答此题采用了“数形结合”的数学思想.

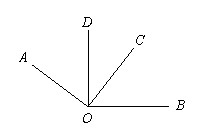
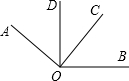
 如图,∠AOC和∠BOD都是直角.
如图,∠AOC和∠BOD都是直角. 解:(1)∵∠AOC是直角,
解:(1)∵∠AOC是直角,

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案