
【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘铭随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)如果该市有8万名初中生,持“无所谓”态度的学生大约有多少人?
【答案】(1)400,图见解析;(2)36°;(3)12000人
【解析】
(1)由条形图可知家长对学生带手机持无所谓态度的有80人,由扇形图可知家长对学生带手机持无所谓态度的占20%,用80÷20%即可算出这次调查的家长人数,再用家长总人数-40-80=家长对学生带手机持反对态度的人数;
(2)根据![]() 计算即可;
计算即可;
(3)算出所调查的学生对持“无所谓”态度的学生所占的百分比,再用此百分比乘以8万即可.
解:(1)80÷20%=400(人),
400-40-80=280(人),
 ;
;
(2)![]() ×100%×360°=36°;
×100%×360°=36°;
(3)![]() ×100%×80000=12000(人),
×100%×80000=12000(人),
答:持“无所谓”态度的学生大约有12000人.


科目:初中数学 来源: 题型:
【题目】综合与探究
数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.
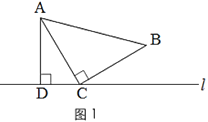
初步探究:
(1)在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由;
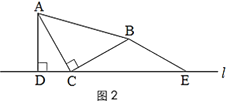
变式拓展:
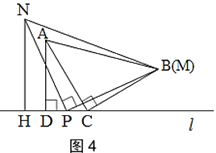
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
请从下面 A,B 两题中任选一题作答,我选择_____题.
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.
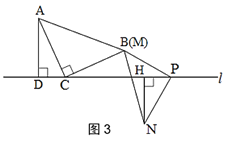
B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AD 是 BC 边上的高,且∠ACB=∠BAD,AE 平分∠CAD,交 BC于点 E,过点 E 作 EF∥AC,分别交 AB、AD 于点 F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF; ③∠BAE=∠BEA; ④∠B=2∠AEF,其中正确的有( )
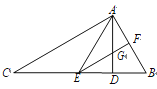
A. 4 个B. 3 个C. 2 个D. 1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来多肉植物风靡全国.花农王大伯分别培植了一批国产多肉与进口多肉.第一次出售国产多肉与进口多肉各100盆,售后发现:国产多肉的平均每盆利润是5元并且始终不变;进口多肉的平均每盆利润是15元,每增加1盆,进口多肉的平均每盆利润增加1元.王大伯计划第二次出售国产多肉与进口多肉共200盆,设进口多肉比第一次增加x盆.
(1)用含x的代数式分别表示第二次国产多肉与进口多肉售完后的利润;
(2)要使第二次国产多肉与进口多肉售完后的总利润比第一次国产多肉与进口多肉售完后总利润多60%,求此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=![]() .其中正确的结论是()
.其中正确的结论是()

A.①②③④B.①④C.①②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:

(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问采用何种购买方案可以使得每月处理污水量的吨数为最多?并求出最多吨数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以顶点A为圆心,AD长为半径,在AB边上截取AE=AD,用尺规作图法作出∠BAD的角平分线AG,若AD=5,DE=6,则AG的长是_________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com