
【题目】如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )

A. B.
B. C.
C. D.
D.
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差 (单位:千克) |
|
|
| 1 | 2 |
箱数 | 2 | 6 | 10 | 8 | 4 |
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,求该市今年居民用水的价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E. 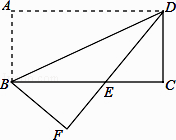
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
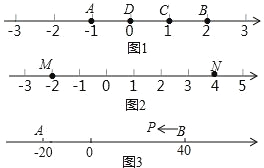
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+1与直线y=﹣ax+c相交于坐标轴上点A(﹣3,0),C(0,1)两点.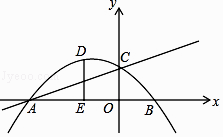
(1)直线的表达式为;抛物线的表达式为 .
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交直线AC于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)P为抛物线上一动点,且P在第四象限内,过点P作PN垂直x轴于点N,使得以P、A、N为顶点的三角形与△ACO相似,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com