
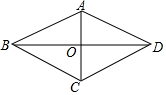
 如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.
如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.分析 (1)根据等腰三角形的性质得到∠ABD=∠ADB,根据角平分线的定义得到∠ABD=∠CBD,等量代换得到∠ADB=∠CBD,根据全等三角形的性质得到AO=OC,于是得到结论;
(2)根据菱形的性质得到OD=$\frac{1}{2}$BD=$\sqrt{5}$,根据勾股定理得到OC=$\sqrt{C{D}^{2}-O{D}^{2}}$=2,于是得到结论.
解答 (1)证明:∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∵AC⊥BD,AB=AD,
∴BO=DO,
在△AOD与△COB中,$\left\{\begin{array}{l}{∠AOD=∠COB}\\{OB=OD}\\{∠ADB=∠CBD}\end{array}\right.$,
∴△AOD≌△COB,
∴AO=OC,
∵AC⊥BD,
∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OD=$\frac{1}{2}$BD=$\sqrt{5}$,
∴OC=$\sqrt{C{D}^{2}-O{D}^{2}}$=2,
∵AC=4,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=4$\sqrt{5}$.
点评 本题考查了菱形的性质和判定,勾股定理,菱形的面积的计算,全等三角形的判定与性质,角平分线的定义,熟练掌握菱形的判定和性质定理是解题的关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
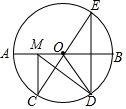 如图,在⊙O中,AB是⊙O的直径,AB=10,$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=$\frac{1}{2}$∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
如图,在⊙O中,AB是⊙O的直径,AB=10,$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=$\frac{1}{2}$∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
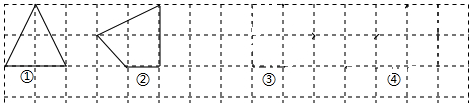
| 图形编号 | 多边形内格点数/个 | 多边形各边上格点数的总和/个 | 多边形的面积/cm2 |
| ① | 1 | 4 | 2 |
| ② | 1 | 5 | $\frac{5}{2}$ |
| ③ | 2 | 10 | 6 |
| ④ | 2 | 4 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明调查了班级里20名同学本学期计划购买课外书的花费情况,并将结果绘制成了扇形统计图.
小明调查了班级里20名同学本学期计划购买课外书的花费情况,并将结果绘制成了扇形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com