
【题目】已知![]() 三个顶点的坐标分别
三个顶点的坐标分别![]() .
.

(1)画出![]() ;
;
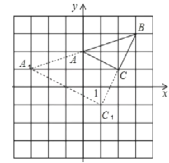
(2)以B为位似中心,将![]() 放大到原来的2倍,在右图的网格图中画出放大后的图形△
放大到原来的2倍,在右图的网格图中画出放大后的图形△![]() ;
;
(3)写出点A的对应点![]() 的坐标:___.
的坐标:___.
【答案】(1)见解析;(2)见解析;(3)(3,1)
【解析】
(1)根据A(0,2)、B(3,3)、C(2,1).在坐标系中找出连接即可;
(2)根据把原三角形的三边对应的缩小或放大一定的比例即可得到对应的相似图形,在改变的过程中保持形状不变(大小可变)即可得出答案.
(3)利用(2)中图象,直接得出答案.
(1)根据A(0,2)、B(3,3)、C(2,1).
在坐标系中找出连接即可;

(2)把原三角形的三边对应的缩小或放大一定的比例即可得到对应的相似图形。
所画图形如下所示:它的三个对应顶点的坐标分别是:(3,1)、(3,3)、(1,1).
(3)利用(2)中图象,直接得出答案.
故答案为:(3,1)


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
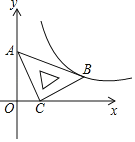
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A.(![]() ,0)B.(2,0)C.(
,0)B.(2,0)C.(![]() ,0)D.(3,0)
,0)D.(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图△ABC中,以AB为直径的⊙O与AC,BC的交点分别为D,E.
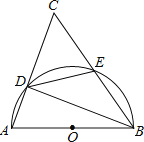
(1)∠A=68°,求∠CED的大小.
(2)当DE=BE时,证明:△ABC为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题发现)如图1,半圆O的直径AB=10,点P是半圆O上的一个动点,则△PAB的面积最大值是 ;

(问题探究)如图2所示,AB、AC、![]() 是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,
是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,![]() 所对的圆心角为60°.新区管委会想在
所对的圆心角为60°.新区管委会想在![]() 路边建物资总站点P,在AB、AC路边分别建物资分站点E、F,即分别在
路边建物资总站点P,在AB、AC路边分别建物资分站点E、F,即分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.显然,为了快捷环保和节约成本,就要使线段PE、EF、FP之和最短(各物资站点与所在道路之间的距离、路宽均忽略不计).可求得△PEF周长的最小值为 km;
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.显然,为了快捷环保和节约成本,就要使线段PE、EF、FP之和最短(各物资站点与所在道路之间的距离、路宽均忽略不计).可求得△PEF周长的最小值为 km;

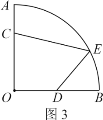
(拓展应用)如图3是某街心花园的一角,在扇形OAB中,∠AOB=90°,OA=12米,在围墙OA和OB上分别有两个入口C和D,且AC=4米,D是OB的中点,出口E在![]() 上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.
上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.
①出口E设在距直线OB多远处可以使四边形CODE的面积最大?最大面积是多少?(小路宽度不计)
②已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元.
请问:在![]() 上是否存在点E,使铺设小路CE和DE的总造价最低?若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.
上是否存在点E,使铺设小路CE和DE的总造价最低?若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为30米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了80米木栏,设这个菜园垂直于墙的一边长为x米.
(1)若平行于墙的一边长为y米,写出y与x的函数表达式子,并求出自变量x的取值范围;
(2)垂直于墙的一边长为多少米时,这个矩形菜园ABCD的面积最大,最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
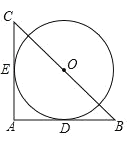
【题目】如图,在 Rt△ABC 中BC=2![]() ,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,
,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.πD.2π
C.πD.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张不透明的卡片,除正面上的图案不同外,其他均相同.将这5张卡片背面向上洗匀后放在桌面上.

(1)从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为_____.
(2)若从中随机抽取1张卡片后不放回,再随机抽取1张,请用画树状图或列表的方法,求两次所抽取的卡片恰好都是轴对称图形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com