练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如下图所示，已知⊙O1与⊙O2相切(包括内切和外切)于点T，求证切点T一定在连心线O1O2上．

    答案：
    解析：

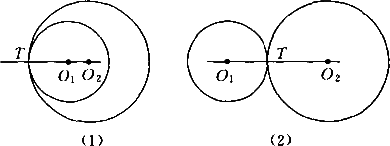
    　　证明：假设切点T不在O1O2上，

    　　∵连心线O1O2是由⊙O1，⊙O2组成的图形的对称轴，

    　　∴点T关于O1O2的对称点也不在O1O2上，

    　　并且也是⊙O1和⊙O2的公共点，

    　　即⊙O1，⊙O2有两个公共点T，．

    　　这与已知⊙O1，⊙O2相切(只有惟一公共点)矛盾．

    　　∴⊙O1，⊙O2相切时，切点T在连心线O1O2上．

    　　说明：(1)要正确区分连心线和圆心距．连心线是指通过不同心的两个圆圆心的一条直线，而圆心距是指两个圆圆心之间的线段的长度，显然两个圆圆心的连线(线段)一定在连心线(直线)上．

    　　(2)“相切两圆的连心线经过切点”也可理解为“相切两圆的圆心、切点在同一条直线上”或“经过相切两圆的切点和一个圆圆心的直线必经过另一个圆的圆心”．

    　　(3)两圆相切时，连心线是常见的一条辅助线，使用连心线时，要注意连心线是直线而不是线段，有时也用圆心距．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    23、如下图所示，已知△ABC，∠C=90°，AC=BC，按下列语句作图（尺规作图，保留痕迹，不必写作法）
    （1）①作∠B的平分线，交AC于D  ②过点D作DE⊥AB，垂足为E
    （2）根据以上所作图形，写出四组相等的线段．（不包括AC=BC）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    26、探究题
    如下图所示，已知平面内A、B、C、D、E五个点．
    （1）按要求画出图形：
    ①画直线AC；
    ②画射线EA、EC；
    ③连接AB、BC、CD、DA．
    （2）在（1）所画的图形中，任意找出一个锐角和一个钝角，并将它们分别表示出来：
    锐角：
    ∠EAC

    钝角：
    ∠AEC

    （3）①用量角器量出四边形AECD的四个内角的度数，即∠DAE、∠AEC、∠ECD、∠CDA的度数分别为
    50°，150°，60°，90°
    ，这四个内角的度数和为
    360°
    ；
    ②用量角器量出四边形ABCD的四个内角的度数，即∠DAB、∠ABC、∠BCD、∠CDA的度数分别为
    90°，70°，110°，90°
    ，这四个内角的度数和为
    360°
    ．从以上的操作中，你有什么发现？（只需写出结论）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    8、如下图所示，已知圆柱的高为8，底面半径为3，若用一个平面沿着上底的直径竖直向下截该圆柱，那么截面的面积为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1997•海南）某公路防护堤的横断面如下图所示．已知斜坡的坡度i=1：1，坡面的铅直高度AC为2m，求斜坡AB的长及其坡角α（答案可保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    甲、乙两所学校中男女生情况如下图所示．已知甲学校有1000人，乙学校有1250人，则甲校与乙校共有男生
    1250
    1250
     人．

    查看答案和解析>>

    同步练习册答案