
 如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.
如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.分析 (1)欲证明AE∥DF,只要证明∠BEA=∠BDF=90°即可.
(2)结论:AF=AB,只要证明四边形AFDC是平行四边形,推出AF=CD,由CD=AB,解决问题.
(3)①如图2中,连接GE.欲证明EI=EA,只要证明∠EIA=∠EAI即可.
②在Rt△DEC中,由DG=GC,推出GE=DG=GC,设GE=a,则DC=2a,首先求出EF,△FEG∽△DCE,得$\frac{EG}{CE}$=$\frac{EF}{CD}$,列出方程求出a2,再根据勾股定理即可解决问题.
解答 解:(1)如图1中,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EF是直径,
∴∠EDF=90°,
∴∠BEA=∠BDF=90°,
∴AE∥DF.
(2)结论:AF=AB.
∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
∵DF∥AC,
∴四边形AFDC是平行四边形,
∴AF=CD,
∴AF=AB.
(3)①如图2中,连接GE.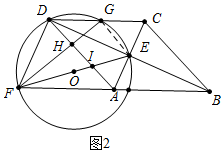
∵EF是直径,
∴∠EGF=90°,
∵DG=GC,EC=AE,
∴GE∥AD,
∴∠EIA=∠FEG,
∵∠ADE+∠DAE=90°,∠GFE+∠FEG=90°,
∵∠CDB=∠BDA=∠EFG,
∴∠DAE=∠FEG,
∴∠DAE=∠EIA,
∴EI=EA.
②在Rt△DEC中,∵DG=GC,
∴GE=DG=GC,设GE=a,则DC=2a,
∵AC=4,AE=EC,
∴EI=EA=2,
∵DF∥AE,
∴∠FDI=∠EAI=∠EIA=∠DIF,
∴DF=IF,由(2)可知DF=AC=4,
∴EF=FI+EI=6,
∵∠EFG=∠CDE,∠FGE=∠DEC=90°,
∴△FEG∽△DCE,
∴$\frac{EG}{CE}$=$\frac{EF}{CD}$,
∴$\frac{a}{2}$=$\frac{6}{2a}$,
∴a2=6,
在Rt△EFG中,FG=$\sqrt{E{F}^{2}-G{E}^{2}}$=$\sqrt{{6}^{2}-6}$=$\sqrt{30}$.
点评 本题考查圆综合题、菱形的性质、平行四边形的判定和性质、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts.
已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-3xy-1是二次三项式 | B. | -x+1是多项式 | ||
| C. | -$\frac{2}{3}$πxy2的系数是-$\frac{2}{3}$π | D. | x与π是同类项 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com