
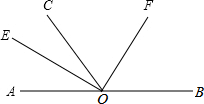
 如图,AOB是一条直线,OC是一条射线,∠AOC=60°,OE、OF分别是∠AOC、∠BOC平分线.
如图,AOB是一条直线,OC是一条射线,∠AOC=60°,OE、OF分别是∠AOC、∠BOC平分线.分析 (1)直接根据角平分线及平角的定义进行解答即可;
(2)有,根据余角的定义进行解答即可.
解答 解:(1)OE⊥OF,
理由:∵OE、OF分别是∠AOC、∠BOC的平分线,∠AOC+∠BOC=180°,
∴∠EOC=$\frac{1}{2}$∠AOC,∠COF=$\frac{1}{2}$∠BOC,
∴∠EOF=∠EOC+∠COF=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$×180°=90°,
∴OE⊥OF.
(2)有,
∠EOC与∠COF,∠EOC与∠BOF,∠COF与∠AOE,∠AOE与∠BOF.
点评 本题考查了角平分线和余角,解决本题的关键是熟记角平分线的定义和余角的定义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
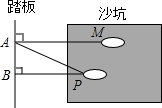 如图,是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.52米,PB=5.37米,MA=5.60米,那么他的跳远成绩应该为5.37米.
如图,是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.52米,PB=5.37米,MA=5.60米,那么他的跳远成绩应该为5.37米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com