
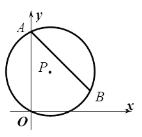
【题目】如图,已知点B(5,2),⊙P经过原点O,交y轴正半轴于点A,点B在⊙P上,∠BAO=45°,圆心P的坐标为____
【答案】![]()
【解析】
连接OP,OB,PB,延长BP交⊙P于E,作EF⊥OA于F,BH⊥x轴于H.利用全等三角形的性质求出点E坐标即可解决问题.
连接OP,OB,PB,延长BP交⊙P于E,作EF⊥OA于F,BH⊥x轴于H.
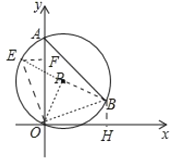
∵∠BPO=2∠BAO,∠BAO=45![]() ,
,
∴∠BPO=90![]() ,
,
∵PO=OB,
∴△PBO是等腰直角三角形,
∵BE是直径,
∴∠BOE=90![]() ,
,
∴∠OBE=∠OEB=45![]() ,
,
∴OE=OB,
∵∠EOB=∠AOH=90![]() ,
,
∴∠EOF=∠BOH,
∵∠EFO=∠BHO=90![]() ,
,
∴△EFO≌△BHO(AAS),
∴OF=OH=5,BF=BH=2,
∴E(2,5),
∵PE=PB,B(5,2)
∴P![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
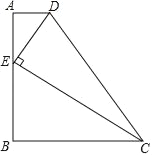
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.
(1)求证:△ADE∽△BEC.
(2)若AD=1,BC=3,AE=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月24日,华为发布旗下最新款折叠屏手机MateX,如图是这款手机的示意图,当两块折叠屏的夹角为30°时(即∠ABC=30°),测得AC之间的距离为40mm,此时∠CAB=45°.求这款手机完全折叠后的宽度AB长是多少?(结果保留整数,参考数据:![]() )
)
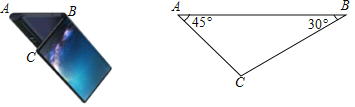
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B是切点,点C是劣弧AB上的一点,若∠P=40°,则∠ACB等于( )
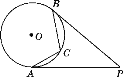
A. 80° B. 110° C. 120° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
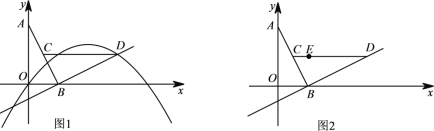
(1)如图1,若该抛物线经过原点O,且a=-![]() .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是3个,请直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,通过画图发现,无论b取何值,抛物线总会经过两个定点;
,通过画图发现,无论b取何值,抛物线总会经过两个定点;
(1)直接写出这两个定点的坐标________ ,_________;
(2)若将此抛物线向右平移![]() 单位,再向上平移
单位,再向上平移![]() (b>0)个单位,平移后的抛物线顶点都在某个函数的图象上,求这个新函数的解析式(不必写自变量取值范围);
(b>0)个单位,平移后的抛物线顶点都在某个函数的图象上,求这个新函数的解析式(不必写自变量取值范围);
(3)若抛物线![]() 与直线y=x–3有两个交点A与B,且
与直线y=x–3有两个交点A与B,且![]() ,求b的取值范围.
,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动.设运动时间为t秒.
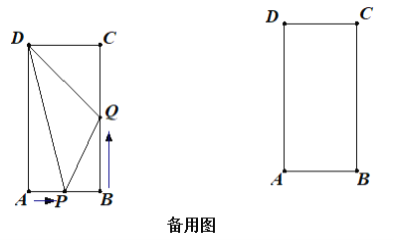
(1)当t=2时,△DPQ的面积为 cm2;
(2)在运动过程中△DPQ的面积能否为26cm2?如果能,求出t的值,若不能,请说明理由;
(3)运动过程中,当 A、P、Q、D四点恰好在同一个圆上时,求t的值;
(4)运动过程中,当以Q为圆心,QP为半径的圆,与矩形ABCD的边共有4个交点时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
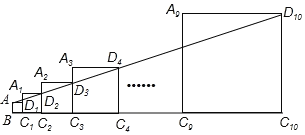
【题目】已知正方形ABC1D1边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图),以比类推……若A1C1=2,且点A、D2,D3,……Dn在同一直线上,则正方形An﹣1Cn﹣1CnDn的边长是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在“中秋”节前购进一种品牌月饼,每盒进价40元,超市规定每盒售价不得低于40元,根据以往销售经验,当售价定为每盒45元时,预计每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求每天的销售量![]() (盒)与售价
(盒)与售价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)如果要保证超市每天的利润为7980元,又要尽量减少库存,超市每天应该销售多少盒月饼?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com