
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点

(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
【答案】(1)y=﹣2x+8;(2)0<x<1或x>3;(3)8.
【解析】试题分析:(1)、首先根据反比例函数的解析式得出点A和点B的坐标,然后根据待定系数法求出一次函数的解析式;(2)、根据函数图形得出答案;(3)、分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点,将△OAB的面积转化成△OAD的面积减去△OBD的面积.
试题解析:(1)、∵点A(m,6),B(3,n)两点在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1,n=2, 即A(1,6),B(3,2). 又∵点A(m,6),B(3,n)两点在一次函数y=kx+b的图象上,
∴![]() . 解得
. 解得![]() , 则该一次函数的解析式为:y=﹣2x+3;
, 则该一次函数的解析式为:y=﹣2x+3;
(2)、根据图象可知使kx+b<![]() 成立的x的取值范围是0<x<1或x>2;
成立的x的取值范围是0<x<1或x>2;
(3)、分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.
令﹣2x+8=0,得x=4,即D(4,0).
∵A(1,6),B(3,2), 则![]() =4×6÷2-4×2÷2=12-4=8
=4×6÷2-4×2÷2=12-4=8


科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO的延长线交⊙O于点F,BP的延长线交AC于点E,连接AP、AF.
(1)求证:AF∥BE;
(2)求证:![]() ;
;
(3)若AB=2,求tan∠F的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
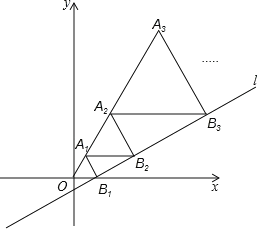
【题目】在直角坐标系中,直线l1:y![]() 与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1,作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3,为边长作等边△A3A2B3…,则等边△A2019A2018B2019的边长是______.
与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1,作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3,为边长作等边△A3A2B3…,则等边△A2019A2018B2019的边长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
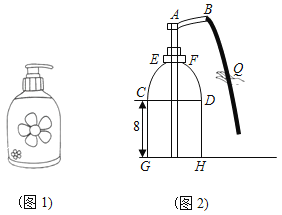
【题目】小林家的洗手盘台面上有一瓶洗手液(如图1).当手按住顶部A下压如图2位置时,洗手液瞬间从喷口B流出路线呈抛物线经过C与E两点.瓶子上部分是由弧![]() 和弧
和弧![]() 组成,其圆心分别为D,C.下部分的是矩形CGHD的视图,GH=10cm,点E到台面GH的距离为14cm,点B距台面的距离为16cm,且B,D,H三点共线.若手心距DH的水平距离为2cm去接洗手液时,则手心距水平台面的高度为_____cm.
组成,其圆心分别为D,C.下部分的是矩形CGHD的视图,GH=10cm,点E到台面GH的距离为14cm,点B距台面的距离为16cm,且B,D,H三点共线.若手心距DH的水平距离为2cm去接洗手液时,则手心距水平台面的高度为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
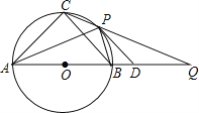
【题目】如图,⊙O为等腰三角形ABC的外接圆,AB是⊙O的直径,AB=12,P为![]() 上任意一点(不与点B,C重合),直线CP交AB的延长线于点Q,⊙O在点P处的切线PD交BQ于点D,则下列结论:①若∠PAB=30°,则
上任意一点(不与点B,C重合),直线CP交AB的延长线于点Q,⊙O在点P处的切线PD交BQ于点D,则下列结论:①若∠PAB=30°,则![]() 的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6
的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6![]() ;④无论点P在
;④无论点P在![]() 上的位置如何变化,CPCQ=108.其中正确结论的序号为 ______.
上的位置如何变化,CPCQ=108.其中正确结论的序号为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com