练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n的值是(　　)

    A. 6 B. 7 C. 8 D. 9

    D 【解析】试题分析：根据从一个n边形的某个顶点出发，可以引（n﹣3）条对角线，把n边形分为（n﹣2）的三角形作答． 【解析】 设多边形有n条边， 则n﹣2=6， 解得n=8． 故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：单选题

    如图，一条流水生产线上L1、L2、L3、L4、L5处各有一名工人在工作，现要在流水生产线上设置一个零件供应站P，使五人到供应站P的距离总和最小，这个供应站设置的位置是(　　)

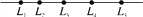
    A. L2处 B. L3处 C. L4处 D. 生产线上任何地方都一样

    B 【解析】试题分析：设在L3处为最佳，求出此时的总距离为L1L5+L2L4，假如设于任意的X处，求出总距离为L1L5+L2L4+L3X，和L1L5+L2L4比较即可． 【解析】 在5名工人的情况下，设在L3处为最佳，这时总距离为L1L5+L2L4， 理由是：如果不设于L3处，而设于X处，则总距离应为L1L5+L2L4+L3X＞L1L5+L2L4， 即在L3处5个工人到供...

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：填空题

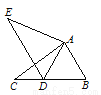
    如图，在△ABC中，AB=4，BC=7，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为__________．

    3 【解析】试题解析: 由旋转的性质可得：AD=AB， ∴△ABD是等边三角形， ∴BD=AB， ∵AB=4，BC=7， ∴CD=BC?BD=7?4=3. 故答案为：3.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：解答题

    如图，△ABC中，AB＝AC＝1，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D。

    （1）求证：BE＝CF ；

    （2）当四边形ACDE为菱形时，求BD的长。

    （1）证明见解析（2）-1 【解析】试题分析：（1）先由旋转的性质得AE=AB，AF=AC，∠EAF=∠BAC，则∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，利用AB=AC可得AE=AF，于是根据旋转的定义，△AEB可由△AFC绕点A按顺时针方向旋转得到，然后根据旋转的性质得到BE=CD； （2）由菱形的性质得到DE=AE=AC=AB=1，AC∥DE，根据等腰三角形的...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：填空题

    对角线长为2的正方形的周长为___________，面积为__________

    2 【解析】根据正方形性质可知：正方形的一条角平分线即为对角线，对角线和正方形的两条相邻的边构成等腰直角三角形，根据勾股定理可知正方形的边长平方是2，即这个正方形的面积为2．正方形的边长是，所以周长是4． 故答案为：4，2．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：单选题

    正方形具有而菱形不具有的性质是

    A．四条边相等 B．对角线互相垂直平分

    C．对角线平分一组对角 D．对角线相等

    D 【解析】 试题分析：正方形的性质四条边相等，四个角相等对角线相等且垂直,互相平分．菱形的性质四条边相等，对角线垂直且互相平分．所以选D．

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型：解答题

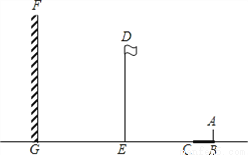
    如图，阳光下，小亮的身高如图中线段AB所示，他在地面上的影子如图中线段BC所示，线段DE表示旗杆的高，线段FG表示一堵高墙．

    （1）请你在图中画出旗杆在同一时刻阳光照射下形成的影子，并用线段表示；

    （2）如果小亮的身高AB=1.6m，他的影子BC=2.4m，旗杆的高DE=15m，旗杆与高墙的距离EG=16m，请求出旗杆的影子落在墙上的长度．

    （1）作图见解析；（2）米. 【解析】试题分析：（1）连接AC，过D点作AC的平行线即可； （2）过M作MN⊥DE于N，利用相似三角形列出比例式求出旗杆的高度即可． 试题解析：（1）如图：线段MG和GE就表示旗杆在阳光下形成的影子． （2）过M作MN⊥DE于N， 设旗杆的影子落在墙上的长度为x，由题意得：△DMN∽△ACB， ∴ 又∵AB=1.6，BC=2...

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：解答题

    把下列各数分别填入相应的集合里．

    ﹣5，﹣2.626 626 662…，0，π，﹣ ，0.12，|﹣6|．

    (1)正数集合：{ …}；

    (2)负数集合：{ …}；

    (3)有理数集合：{ …}；

    (4)无理数集合：{ …}．

    π，0.12，|﹣6|；﹣5，﹣2.626 626 662…，﹣；﹣5，0，﹣，0.12，|﹣6|；﹣2.626 626 662…，π． 【解析】试题分析：依据正数，负数数，有理数，无理数的概念判断即可. 试题解析： 正数集合： 负数集合： 有理数集合： 无理数集合：

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：单选题

    在等腰直角三角形ABC中，AB=AC=4，点O为BC的中点，以O为圆心作半径交BC于点M、N，半圆O与AB、AC相切，切点分别为D、E，则半圆O的半径和的度数分别为（ ）

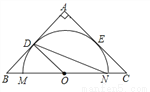
    A. 2，22.5° B. 3，30° C. 3，22.5° D. 2，30°

    A 【解析】试题分析：∵△ABC为等腰直角三角形， ∴BC＝AB＝，∠B＝45°， ∵点O为BC的中点， ∴OB＝， ∵AB为切线， ∴OD⊥AB， ∴∠ODB＝90°， ∴△ODB为等腰直角三角形， ∴OD＝OB＝×＝2，∠BOD＝45°， ∴∠MND＝∠BOD＝22.5°． 故选A．

    查看答案和解析>>

    同步练习册答案