
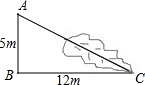
 如图,一棵大树折断后倒在地上,根据图中数据计算大树没折断时的高度是18m.
如图,一棵大树折断后倒在地上,根据图中数据计算大树没折断时的高度是18m. 科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
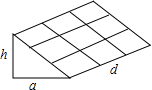 如图,要修建一个育苗棚,棚高h=3m,棚宽a=4m,棚长d=12m,现要在育苗棚的整个表面(除底面外所有的面)覆盖一层塑料薄膜,试求至少需要多少平方米塑料薄膜?(接缝处不计)
如图,要修建一个育苗棚,棚高h=3m,棚宽a=4m,棚长d=12m,现要在育苗棚的整个表面(除底面外所有的面)覆盖一层塑料薄膜,试求至少需要多少平方米塑料薄膜?(接缝处不计)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
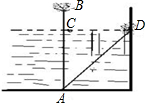 水池中离岸边D点1.5米的C处,直立长着一根芦苇,出水部分BC的长是0.5米,把芦苇拉到岸边,它的顶端B恰好落到D点,并求水池的深度AC.
水池中离岸边D点1.5米的C处,直立长着一根芦苇,出水部分BC的长是0.5米,把芦苇拉到岸边,它的顶端B恰好落到D点,并求水池的深度AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,用直尺和圆规作∠PCD=∠AOB,作图痕迹中,弧$\widehat{MN}$是( )
如图,用直尺和圆规作∠PCD=∠AOB,作图痕迹中,弧$\widehat{MN}$是( )| A. | 以点C为圆心,OE为半径的弧 | B. | 以点C为圆心,EF为半径的弧 | ||
| C. | 以点G为圆心,OE为半径的弧 | D. | 以点G为圆心,EF为半径的弧 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com