
【题目】如图1,在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于
轴于![]() 、
、![]() 两点,已知
两点,已知![]() 点坐标
点坐标![]() ,点
,点![]() 在直线
在直线![]() 上,横坐标为
上,横坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上的一个动点,连结
轴正半轴上的一个动点,连结![]() ,以
,以![]() 为直角边在右侧构造一个等腰
为直角边在右侧构造一个等腰![]() ,且
,且![]() .
.
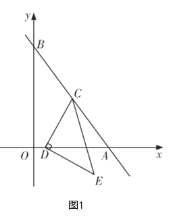

(1)求直线![]() 的解析式以及
的解析式以及![]() 点坐标;
点坐标;
(2)设点![]() 的横坐标为
的横坐标为![]() ,试用含
,试用含![]() 的代数式表示点
的代数式表示点![]() 的坐标;
的坐标;
(3)如图2,连结![]() ,
,![]() ,请直接写出使得
,请直接写出使得![]() 周长最小时,点
周长最小时,点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)用待定系数法求出直线![]() 的解析式后,将x=3代入即可;
的解析式后,将x=3代入即可;
(2)作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,根据AAS可证
,根据AAS可证![]() ,即可得E点坐标;
,即可得E点坐标;
(3)将![]() 周长最小转化为和最小问题,利用对称性进行解答即可.
周长最小转化为和最小问题,利用对称性进行解答即可.
解:(1)把![]() 代入
代入![]() 中,
中,
得![]() ,解得
,解得![]() ,
,
![]() ,
,
把![]() 代入,得
代入,得![]() ,
,
![]()
(2)作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,
![]() 是等腰
是等腰![]() ,
,
![]() ,
,![]() ,
,
![]() ,且
,且![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]()
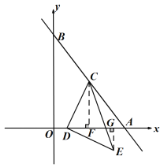
(3)∵![]()
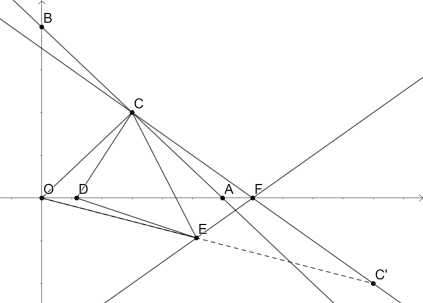
∴E在函数y=x-7图像上运动
作C关于直线y=x-7的对称点![]() ,连接
,连接![]() 交 直线y=x-7于F,则
交 直线y=x-7于F,则![]() ,F为
,F为![]() 的中点,
的中点,![]()
∴当![]() 三点共线时
三点共线时 ![]() 周长最小,
周长最小,
∴![]() 周长最小为:
周长最小为:![]()
∴设![]()
把C(3,4)代入![]() 得:4=-3+b
得:4=-3+b
解得:b=7
∴![]()
∵![]()
∴![]()
∴F(7,0)
∵F为![]() 的中点,C(3,4),F(7,0)
的中点,C(3,4),F(7,0)
∴![]()
连接![]() ,设直线
,设直线![]() 的解析式为:
的解析式为:![]()
把![]() 代入
代入![]() 得:
得:![]()
解得![]()
∴![]()
∴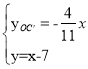
解得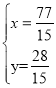
∴![]() .
.
∴![]() 周长最小时:
周长最小时:![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,点D,E,F分别是△ABC三边的中点,则下列判断错误的是( )
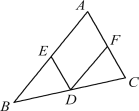
A. 四边形AEDF一定是平行四边形 B. 若AD平分∠A,则四边形AEDF是正方形
C. 若AD⊥BC,则四边形AEDF是菱形 D. 若∠A=90°,则四边形AEDF是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位老师同住一小区,该小区与学校相距![]() 米.甲从小区步行去学校,出发
米.甲从小区步行去学校,出发![]() 分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为
分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为![]() 米/分,甲步行的速度比乙步行的速度每分钟快
米/分,甲步行的速度比乙步行的速度每分钟快![]() 米.设甲步行的时间为
米.设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 与折线
与折线![]() 分别表示甲、乙离小区的路程
分别表示甲、乙离小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
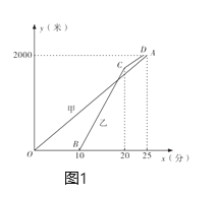
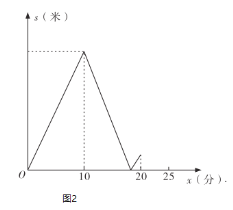
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求直线![]() 的解析式;
的解析式;
(3)在图2中,画出当![]() 时,
时,![]() 关于
关于![]() 的函数的大致图象.
的函数的大致图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形中点的个数,其中第一个图形中共有4个点,第2个图形中共有10个点,第3个图形中共有19个点,…按此规律第6个图形中共有点的个数是( )
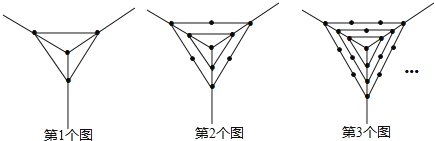
A.38B.46C.61D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)(﹣![]() a6x5y4)÷(﹣3a2xy2)×(﹣
a6x5y4)÷(﹣3a2xy2)×(﹣![]() ax)2
ax)2
(3)[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x
查看答案和解析>>
科目:初中数学 来源: 题型:
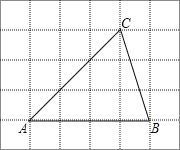
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)△ABC的面积等于_____;
(Ⅱ)若四边形DEFG是正方形,且点D,E在边CA上,点F在边AB上,点G在边BC上,请在如图所示的网格中,用无刻度的直尺,画出点E,点G,并简要说明点E,点G的位置是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.
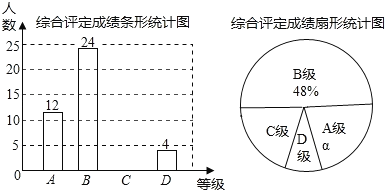
请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生;
(2)a= %;C级对应的圆心角为 度.
(3)补全条形统计图;
(4)若该校共有2000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com