
����Ŀ�����������ij��¥�ݹ���10��̨�ף����ijͬѧ����̨��ʱ������һ��1��̨�ף�Ҳ����һ��2��̨�ף���ô��ͬѧ�Ӹö�¥�ݵײ��ϵ��������ж����ֲ�ͬ���߷���
����̽����
Ϊ�������ʵ�����⣬�����Ƚ���������ѧģ�ͣ�
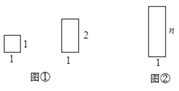
��ͼ�٣������ɸ��߳���Ϊ1�������Σ���Ϊ1��1���Σ������ɸ��߳��ֱ�Ϊ1��2�ľ��Σ���Ϊ1��2���Σ���Ҫƴ��һ����ͼ���б߳��ֱ�Ϊ����n�ľ��Σ���Ϊ1��![]() ���Σ����ж����ֲ�ͬ��ƴ��������
���Σ����ж����ֲ�ͬ��ƴ��������![]() ��ʾ��ͬƴ���ĸ�����
��ʾ��ͬƴ���ĸ�����
Ϊ���������ѧģ�����⣬���Dz�ȡ�IJ��Ժͷ����ǣ�һ���������⻯��
̽��һ���ȴ���������������֣���Ҫƴ��һ��1��1���Σ��ж����ֲ�ͬƴ����
��Ȼ��ֻ��1��ƴ������ͼ�ۣ���![]() =1�֣�
=1�֣�
̽������Ҫƴ��һ��1��2���Σ��ж����ֲ�ͬƴ����
���Կ�������2��ƴ������ͼ�ܣ���![]() =2�֣�
=2�֣�
̽������Ҫƴ��һ��1��3���Σ��ж����ֲ�ͬƴ����
ƴͼ�����ɷ�Ϊ���ࣺһ������ͼ����2��1��2�����Ϸ�����ƴ��һ��1��1���Σ�������ƴ������![]() =2�֣���һ������ͼ���⣱��1��1�����Ϸ�ƴ��һ��1��2���Σ�������ƴ����
=2�֣���һ������ͼ���⣱��1��1�����Ϸ�ƴ��һ��1��2���Σ�������ƴ����![]() =1�֣���ͼ�ݣ���
=1�֣���ͼ�ݣ���![]() =
=![]() +
+![]() = 2+1=3���֣���
= 2+1=3���֣���
![]()
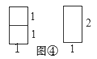
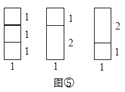
̽���ģ���������̽�����̣�Ҫƴ��һ��1��4���Σ��ж����ֲ�ͬƴ�����뻭ʾ��ͼ˵������������
̽���壺Ҫƴ��һ��1��5���Σ���������̽�����̣��ó�![]() =�������� �ֲ�ͬƴ����
=�������� �ֲ�ͬƴ����
��ֱ��д����������軭ͼ����
��������������������е���ѧģ�ͣ����������������е�ʵ�����⣮
��д�������̣����軭ͼ����
���𰸡�̽���ģ�5; ̽����:8,89
������������ͼ���о�����Ϲ��ɵó�A1��5=A1��3+A1��4��A1��n=A1����n��1��+A1����n��2��������������ɣ�
̽������

ƴͼ�����ɷ�Ϊ������һ������ͼ����2��1��2�����Ϸ�����ƴ��һ��1��2������������ƴ������A1��2 =2������һ������ͼ����3��1��3�����Ϸ�����ƴ��һ��1��1������������ƴ������A1��3 =3��������ͼ����A1��4 =![]() +
+![]() =3+2=5���֣���
=3+2=5���֣���
̽��������A1��4=A1��2+A1��3=5��A1��5=A1��3+A1��4=3+5=8����Ҫƴ��һ��1��5��������8�ֲ�ͬƴ��A1��5��
�ʴ�Ϊ��8��
����������¥�ݹ���10��̨�������ijͬѧ����̨��ʱ������һ��1��̨����Ҳ����һ��2��̨����A1��1=1������A1��3=A1��2+A1��1=2+1=3���֣���A1��4=A1��3+A1��2=3+2=5���֣���A1��5=8���֣�����A1��6=A1��4+A1��5=5+8=13��A1��7=A1��6+A1��5=13+8=21����A1��8=A1��6+A1��7=13+21=34����A1��9=A1��7+A1��8=21+34=55����A1��10=A1��8+A1��9=34+55=89��
������ͬѧ�Ӹö�¥�ݵײ��ϵ���������89�ֲ�ͬ���߷���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx(a��0) ��x���������ڵ�A��ֱ��y=2x ���������ߵĶ���M����֪�������ߵĶԳ���Ϊֱ��x=2����x���ڵ�B��
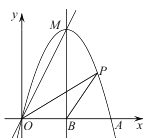
��1����a��b��ֵ��
��2��P�ǵ�һ�������������ϵ�һ�㣬���ڶԳ�����Ҳ࣬����OP��BP�����P�ĺ�����Ϊm ����OBP�����ΪS��![]() ����K����m �ĺ�������ʽ��K�ķ�Χ��
����K����m �ĺ�������ʽ��K�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��ֱ��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ����
����![]() �ᣬ
�ᣬ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ����
����![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.

��1�����![]() ����
����![]() ����
����![]() �����꣬�����
�����꣬�����![]() �������
�������
��2����ֱ�� ![]() �ϴ��ڵ�
�ϴ��ڵ�![]() ������
������![]() �غϣ�������
�غϣ�������![]() ���������
���������![]() �����ꣻ
�����ꣻ
��3����![]() ���Ҳ���һ��ֱ��ƽ����
���Ҳ���һ��ֱ��ƽ����![]() �ᣬ�ֱ���
�ᣬ�ֱ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ���ҵ�
���ҵ�![]() �ڵ�
�ڵ�![]() ���·���
���·���![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ
��ʹ![]() Ϊ����ֱ�������Σ������ڣ���ֱ��д�����������ĵ�
Ϊ����ֱ�������Σ������ڣ���ֱ��д�����������ĵ�![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ�ѧУ���еĴ�ͳ�Ļ�֪ʶ������ij��������Ĵ�ģ��ѵ�������ɼ�����������������ʻ��Ƴ�����������������ͳ��ͼ��
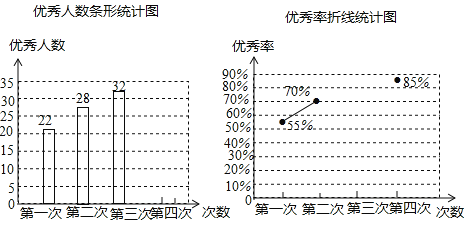
��1�����������
��2�����ݼ��㣬���㲹ȫ����ͳ��ͼ��
��3����֪�ð��ͬѧ�Ĵ�ѵ���ɼ�Ϊ85��95��85��95����ͬѧ�Ĵγɼ��ֱ�Ϊ85��90��95��90������Ӽס�����ͬѧ��ѡ��һ��ͬѧ�μ�У������������ΪӦ��ѡ����λͬѧ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��L��y=3x+2�������������⣺
�ٹ���P��-1��1����ֱ��Lƽ�е�ֱ����y=3x+4������ֱ��L��x�ᡢy��ֱ���A��B���㣬��AB=![]() ��������M��-
��������M��-![]() ��1����N��a��b������ֱ��L�ϣ���a>-
��1����N��a��b������ֱ��L�ϣ���a>-![]() ����b>1�� ������Q����������ľ�����ȣ���Q��L�ϣ����Q�ڵ�һ��ڶ����ޡ�������ȷ��������_________��
����b>1�� ������Q����������ľ�����ȣ���Q��L�ϣ����Q�ڵ�һ��ڶ����ޡ�������ȷ��������_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����ij�г˳����������y��Ԫ�����г����x��km��֮��ĺ�����ϵͼ��
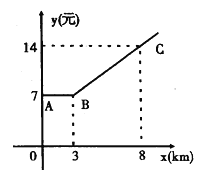
��1������ͼ����x��3ʱ�ĺ�����ϵʽ��
��2��ij�˳���2.5km��Ӧ������Ǯ��
��3��ij�˳���13km��Ӧ������Ǯ��
��4����ij�˸�����30.8Ԫ�������ʻ�˶���·�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ƽ��
ƽ��![]() ��
��
��1����![]() ��
��![]() ����
����![]() �Ķ�����
�Ķ�����
��2����![]() ƽ��
ƽ��![]() ��
��![]() ����
����![]() ��
��
����֤![]() ��
��
����![]() �Ķ�����
�Ķ�����
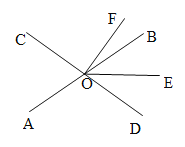
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC�У�AB=AC��D��BC���е㣬��E��AD��.
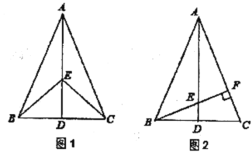
��1����֤��BE=CE��
��2����ͼ2����BE���ӳ��߽�AC�ڵ�F����BF��AC������ΪF����BAC=45����ԭ����������������.��֤��EF=CF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���֪��A����3��3����B����5��1����C����2��0����P��a��b������ABC�ı�AC������һ�㣬��ABC����ƽ�ƺ�õ���A1B1C1����P�Ķ�Ӧ��ΪP1��a+6��b��2����
��1��ƽ�ƺ��������������ֱ�Ϊ��.A1�� ����B1�� ����C1�� ��.
��2������ͼ�л���ƽ�ƺ�������A1B1C1��
��3��������AOA1�������AOA1�������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com