
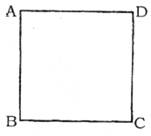
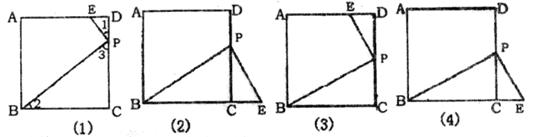
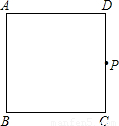
操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角形的直角顶点与点P重合,并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线相交于点E。
探究:(1)观察操作结果,哪一个三角形与△BPC相似?说明你的理由;
(2)当点P位于CD的中点时,你找到的(1)中三角形与△BPC的周长比是多少?
解:(1)如图(1),另一条直角边与AD交于点E,则△PDE∽△BCP
证明:在△PDE和△BCP中,
∵∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2
又∠PDE=∠BCP=90°,
∴△PDE∽△BCP
或:如图(2),若另一条直角边与BC的延长线交于点E,
同理可证△PCE∽△BCP
或:如图(2),若另一条直角边与BC的延长线交于点E,
同理可证△BPE∽△BCP
(3)如图(3),当点P位于CD的中点时,若另一条直角边与AD交于点E,则![]()
又∵△PDE∽△BCP
∴△PDE与△BCP的周长比是12
或:如图(4),若另一条直角边与BC的延长线交于点E,同理可证
△PCE与△BCP的周长比是12
或:若一条直角边与BC的延长线交于点E,
∵![]()
又△BPE∽△BCP
∴△BPE与△BCP的周长比是![]() 2
2


科目:初中数学 来源: 题型:
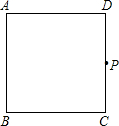 操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与点P重合(含30度角的直角三角板),并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.
操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与点P重合(含30度角的直角三角板),并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.查看答案和解析>>
科目:初中数学 来源:2012年河北省石家庄市42中学九年级第二次模拟考试数学试卷(带解析) 题型:解答题
操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与点P重合,并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.
探究:①观察操作结果,哪一个三角形与△BPC相似,写出你的结论,(找出两对即可);并选择其中一组说明理由;
②当点P位于CD的中点时,直接写出① 中找到的两对相似三角形的相似比和面积比.
查看答案和解析>>
科目:初中数学 来源:2012年河北省石家庄市九年级第二次模拟考试数学试卷(解析版) 题型:解答题
操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与点P重合,并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.
探究:①观察操作结果,哪一个三角形与△BPC相似,写出你的结论,(找出两对即可);并选择其中一组说明理由;
②当点P位于CD的中点时,直接写出① 中找到的两对相似三角形的相似比和面积比.

查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《图形的相似》(05)(解析版) 题型:解答题
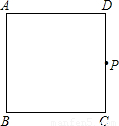
查看答案和解析>>
科目:初中数学 来源:2003年云南省昆明市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com