Question

15．探究：
将一个正方体表面全部涂上颜色，试回答：
（1）把正方体的棱三等分，然后沿等分线把正方体切开，得到27个小正方体，我们把仅有i个面涂色的小正方体的个数记为x_i，那么x₃=8，x₂=12，x₁=6，x₀=1；
（2）如果把正方体的棱四等分，同样沿等分线把正方体切开，得到64个小正方体，与（1）同样的记法，则x₃=8，x₂=24，x_l=24，x₀=8；
（3）如果把正方体的棱n等分（n≥3），然后沿等分线把正方体切开，得到n³个小正方体，与（1）同样的记法，则x₃=8，x₂=12（n-2），x₁=6（n-2）²，x₀=（n-2）³．

Answer 1

分析 （1）根据图示：在原正方体的8个顶点处的8个小正方体上，有3个面涂有颜色；2个面涂有颜色的小正方体在每条棱的中间，共有12个；1个面涂有颜色的小正方体有6个，分布在每个面的中心；没有涂上颜色的小正方体有1个，在原正方体的中心．
（2）根据图示可发现定点处的小方块三面涂色，除顶点外位于棱上的小方块两面，涂色位于表面中心的一面涂色，而处于正中心的则没涂色．
（3）由特殊推广到一般即可得到n等分时所得小正方体表面涂色情况．

解答 解：（1）根据长方体的分割规律可得x₃=8，x₂=12，x₁=6，x₀=1．
故答案为8，12，6，1．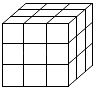

（2）把正方体的棱四等分时，顶点处的小正方体三面涂色共8个；有一条边在棱上的正方体有24个，两面涂色；每个面的正中间的4个只有一面涂色，共有24个；正方体正中心处的8个小正方体各面都没有涂色．故x₃=8，x₂=24，x₁=24，x₀=8．
故答案为8，24，24，8．
（3）由以上可发现规律：三面涂色x₃8个，两面涂色x₂=12（n-2）个，一面涂色x₁=6（n-2）²个，各面均不涂色x₀=（n-2）³个．
故答案为8，12（n-2），6（n-2）²，（n-2）³．

点评 主要考查了立体图形的认识和用特殊归纳一般规律的方法．关键是通过正方体的特点来得到有关涂色情况的规律．