练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
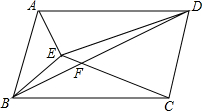
    5．如图，点E在平行四边形ABCD内，连结EA、EB、EC、ED，其中EC与对角线BD交于点F，则S△ABE+S△DEF=（　　）
    A．S△AEDB．S△ECDC．$\frac{1}{4}$S?ABCDD．S△BCF

    分析 由平行四边形的性质得出△ABE的面积+△CDE的面积=△BCD的面积，得出△ABE的面积+△CDE的面积-△CDF的面积=△BCD的面积-△CDF的面积，即可得出结果．

    解答 解：∵四边形ABCD是平行四边形，
    ∴△ABE的面积+△CDE的面积=$\frac{1}{2}$平行四边形ABCD的面积，△BCD的面积=$\frac{1}{2}$平行四边形ABCD的面积，
    ∴△ABE的面积+△CDE的面积=△BCD的面积，
    ∴△ABE的面积+△CDE的面积-△CDF的面积=△BCD的面积-△CDF的面积，
    即S△ABE+S△DEF=S△BCF；
    故选：D．

    点评 本题考查了平行四边形的性质、三角形的面积关系；熟练掌握平行四边形的性质，得出△ABE的面积+△CDE的面积=△BCD的面积是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮后就会有121台电脑被感染，请用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？若病毒得不到有效控制，3轮后，被感染的电脑会不会超过1000台？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．解不等式组：$\left\{\begin{array}{l}{2x-（x-2）＞4}\\{\frac{1-2x}{3}≤x-1}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．在△ABC中，AB=BC，∠A=61°，F是AB上的一点，过点F作FE∥BC交AC于点E，过点E作ED∥AB交BC于点D，则∠AEF+∠CED=122°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．甲、乙两人要从A地到B地，乙步行2小时后，甲骑自行车以25千米/时的速度沿同一路线追击，45分钟后甲超过乙5千米，求乙的速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．某中学在一次八年级数学单元测试中，随机抽取了8%的学生的数学成绩进行分析，现将他们的成绩分成A（85～100分），B（70～84分），C（60～69分），D（60分以下）四个等级进行分析，再制成如图两个统计图，已知在所抽取的学生中，D级的学生有4人．

    （1）所抽取的学生中数学成绩的中位数落在哪个等级中？请说明理由．
    （2）所抽取的学生的数学平均成绩是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．若|2x-5|=5-2x，则x的取值范围是x≤$\frac{5}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．求$\sqrt{（x-3）^{2}+4}$+$\sqrt{{x}^{2}+1}$的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．若代数式m2-1999m+1998的值为0，则m的值为1或1998．

    查看答案和解析>>

    同步练习册答案