

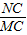 =
= ,CM=
,CM=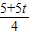 ;
; (1+t)+1+t=
(1+t)+1+t= (3+4+5),
(3+4+5), .(5分)
.(5分) NC=
NC= (1+t),
(1+t),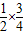 (1+t)2=
(1+t)2= (1+t)2,
(1+t)2, 时,S△MNC=
时,S△MNC= (1+t)2=
(1+t)2= ≠
≠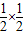 ×4×3.
×4×3. ;
; (1+t)=4-t,
(1+t)=4-t,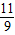 ;
;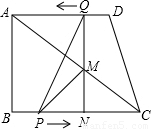 ③当PM=PC时;则有:在Rt△MNP中,PM2=MN2+PN2,
③当PM=PC时;则有:在Rt△MNP中,PM2=MN2+PN2, NC=
NC= (1+t),
(1+t), (1+t)]2+(3-2t)2=(4-t)2,
(1+t)]2+(3-2t)2=(4-t)2,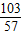 ,t2=-1(舍去)
,t2=-1(舍去) ,t=
,t=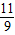 ,t=
,t= 时,△PMC为等腰三角形.
时,△PMC为等腰三角形.

科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(08)(解析版) 题型:解答题
 ,求矩形ABCD的面积.
,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:2010年山东省德州市武城县九年级练兵考试数学试卷(一)(解析版) 题型:解答题
 ,求矩形ABCD的面积.
,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:2009年湖北省江汉油田中考数学试卷(解析版) 题型:解答题
 ,求矩形ABCD的面积.
,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《图形的平移》(01)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com