
【题目】已知:如图12①、②、③,在矩形ABCD中,AB=4,BC=8,P是边BC上的一个动点.
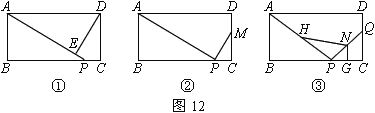
(1)如图①,若DE⊥AP,垂足为E,求证:△AED∽△PBA
(2)如图②,在(1)的条件下,将DE沿AP方向平移,使P、E两点重合,且与边CD的交点为M,若MC=3,求BP的长.
(3)如图③,Q是边CD上的一个动点,若![]() =2,且H,N,G分别为AP,PQ,PC的中点,请问:在P、Q两点分别在BC、CD上运动的过程中,四边形HPGN的面积是否发生变化?若变化,请说明理由,若不变化,请求出它的面积.
=2,且H,N,G分别为AP,PQ,PC的中点,请问:在P、Q两点分别在BC、CD上运动的过程中,四边形HPGN的面积是否发生变化?若变化,请说明理由,若不变化,请求出它的面积.
【答案】(1)见解析;(2)BP的长为2或6;(3)四边形HPGN的面积不会发生变化,它的面积是4
【解析】
(1)根据题意知∠DAE=∠APB,利用DE⊥AP,∠B=90°,即可得到△AED∽△PBA;
(2)根据题意可以证得△APB∽△PMC,设BP=x,则PC=8-x,利用相似的性质![]() =
=![]() ,将对应的线段值代入进去,列出方程即可求解;
,将对应的线段值代入进去,列出方程即可求解;
(3)根据题意设设CQ=k,则BP=2k,过点H作HF⊥BC于F,可证得△PHF∽△PAB,得出HF=![]() AB=2,PF=
AB=2,PF=![]() PB=k,利用三角形中位线性质可得△PNG∽△PQC,得出PG=4-k,NG=4,从而表示出四边形HPGN的面积即可.
PB=k,利用三角形中位线性质可得△PNG∽△PQC,得出PG=4-k,NG=4,从而表示出四边形HPGN的面积即可.
证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAE=∠APB.
又∵DE⊥AP,
∴∠DEA=90°,
∴∠DEA=∠B,
∴△AED∽△PBA.
(2)由题意知MP⊥AP,
∴∠APM=90°,
∴∠APB+∠MPC=90°.
又∵∠APB+∠PAB=90°,
∴∠APB=∠PMC.
∵∠B=∠C=90°,
∴△APB∽△PMC,
∴![]() =
=![]() .
.
设BP=x,则PC=8-x,
∴![]() =
=![]() ,
,
解得x=2或6,
∴BP的长为2或6.
(3)因为![]() =2,设CQ=k,则BP=2k.
=2,设CQ=k,则BP=2k.

如图,过点H作HF⊥BC于F,
又∵AB⊥BC,
∴HF∥AB,
∴△PHF∽△PAB,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴HF=![]() AB=2,PF=
AB=2,PF=![]() PB=k.
PB=k.
∵N、G分别是PQ,PC的中点,
∴NG∥QC,
∴△PNG∽△PQC,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴PG=![]() PC=
PC=![]() ( BC-BP)=4-k,NG=CQ=k.
( BC-BP)=4-k,NG=CQ=k.
∴S四边形HPGN=S梯形HFGN-S△HFP=![]() (
(![]() k+2)(4-k+k)-
k+2)(4-k+k)-![]() ×2k=k+4-k=4.
×2k=k+4-k=4.
所以,四边形HPGN的面积不会发生变化,它的面积是4.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,且AD//BC,BD的垂直平分线经过点O,分别与AD、BC交于点E、F
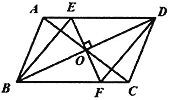
(1)求证:四边形ABCD为平行四边形;
(2)求证:四边形BFDE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的直径
的直径![]() ,半径
,半径![]() ,
,![]() 为
为![]() 上一动点(不包括
上一动点(不包括![]() 两点),
两点),![]() ,垂足分别为
,垂足分别为![]() .
.

(1)求![]() 的长.
的长.
(2)若点![]() 为
为![]() 的中点,
的中点,
①求劣弧![]() 的长度,
的长度,
②者点![]() 为直径
为直径![]() 上一动点,直接写出
上一动点,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.


请结合统计图,回答下列问题:
(1)本次调查学生共 人, ![]() = ,并将条形图补充完整;
= ,并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校让每班在A、B、C、D四钟活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,AB=DC,P为梯形ABCD外一点,PA、PD分别交线段BC于点E、F,且PA=PD.

(1)写出三对你认为全等的三角形(不再添加辅助线);
(2)选择你在(1)中写出的全等三角形中的任意一对进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产并进行治污改造,其月利润![]() (万元)与月份
(万元)与月份![]() 之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )

A.4月份的利润为![]() 万元
万元
B.污改造完成后每月利润比前一个月增加![]() 万元
万元
C.治污改造完成前后共有![]() 个月的利润低于
个月的利润低于![]() 万元
万元
D.9月份该厂利润达到![]() 万元
万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .点
.点![]() 在函数图像上,
在函数图像上,![]() 轴,且
轴,且![]() ,直线
,直线![]() 是抛物线的对称轴,
是抛物线的对称轴,![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求![]() 、
、![]() 的值;
的值;
(2)如图①,连接![]() ,线段
,线段![]() 上的点
上的点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在线段
恰好在线段![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)如图②,动点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线分别与
轴的垂线分别与![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() .试问:抛物线上是否存在点
.试问:抛物线上是否存在点![]() ,使得
,使得![]() 与
与![]() 的面积相等,且线段
的面积相等,且线段![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
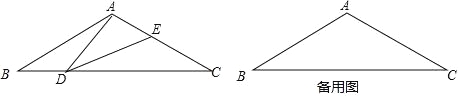
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com