
| A. H | B. U | C. A | D. N |
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
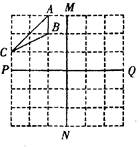
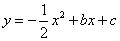 与x轴交于A(1,0)、
与x轴交于A(1,0)、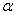 (0°<
(0°<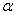 <90°)
<90°)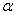 等于多少度时,△CPQ是等腰三角形?
等于多少度时,△CPQ是等腰三角形?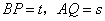 ,求s与t之间的函数关系式.
,求s与t之间的函数关系式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
. ;(不要求写作法)
;(不要求写作法) )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG.
FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com