
【题目】将代数式4a2b+3ab2﹣2b2+a3按a的升幂排列的是( )
A.﹣2b3+3ab2+4a2b+a3
B.a3+4a2b+3ab2﹣2b3
C.4a2b+3ab2﹣2b3+a3
D.4a2b+3ab2+a3﹣2b3
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】把下列各数填入表示它所在的数集的括号里.
﹣5, ![]() ,0.62,4,0,﹣6.4,
,0.62,4,0,﹣6.4, ![]() ,20%,﹣2010,
,20%,﹣2010, ![]() ,﹣|﹣(+7.6)|,π.
,﹣|﹣(+7.6)|,π.
(1)有理数集合{ };
(2)整数集合{ };
(3)非负分数集合{ };
(4)自然数集合{ }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(时)之间的关系如图所示.以下说法错误的是( )
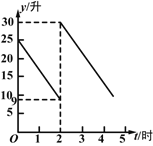
A. 加油前油箱中剩余油量y(升)与行驶时间t(时)之间的函数关系式是y=-8t+25
B. 途中加油21升
C. 汽车加油后还可行驶4小时
D. 汽车到达乙地时油箱中还余油6升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+bx+![]() (a≠0)经过点A(-1,0)和B(3,0).
(a≠0)经过点A(-1,0)和B(3,0).

(1)求抛物线C1的解析式,并写出其顶点C的坐标;
(2)如图1,把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2,此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴的下方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标;
(3)如图2,在(2)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时:
①tan∠ENM的值如何变化?请说明理由;
②点M到达点C时,直接写出点P经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的边BA延长到点E,使AE=AB,连接EC,交AD于点F,连接AC、ED. 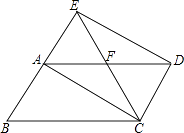
(1)求证:四边形ACDE是平行四边形;
(2)若∠AFC=2∠B,求证:四边形ACDE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司将5名员工分配至3个不同的部门,每个部门至少分配一名员工,其中甲、乙两名员工必须分配在同一个部门的不同分配方法数为( )
A.24
B.30
C.36
D.42
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足 ![]() +(b2﹣16)2=0.
+(b2﹣16)2=0. 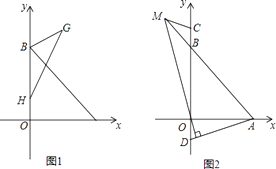
(1)求A、B两点的坐标,∠OAB的度数;
(2)如图1,已知H(0,1),在第一象限内存在点G,HG交AB于E,使BE为△BHG的中线,且S△BHE=3,
①求点E到BH的距离;
②求点G的坐标;
(3)如图2,C,D是y轴上两点,且BC=OD,连接AD,过点O作MN⊥AD于点N,交直线AB于点M,连接CM,求∠ADO+∠BCM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:三边长和面积都是整数的三角形称为“整数三角形”. 数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
(1)请你画出小颖和小辉摆出的“整数三角形”的示意图;
(2)你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由. ①摆出等边“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com