
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的 ![]() 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大 ![]() 倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 . 
【答案】(﹣ ![]() ,
, ![]() )
)
【解析】解:∵在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的 ![]() 倍,
倍,
∴矩形A1OC1B1与矩形AOCB是位似图形,点B与点B1是对应点,
∵OA=2,OC=1.
∵点B的坐标为(﹣2,1),
∴点B1的坐标为(﹣2× ![]() ,1×
,1× ![]() ),
),
∵将矩形A1OC1B1以原点O为位似中心放大 ![]() 倍,得到矩形A2OC2B2…,
倍,得到矩形A2OC2B2…,
∴B2(﹣2× ![]() ×
× ![]() ,1×
,1× ![]() ×
× ![]() ),
),
∴Bn(﹣2× ![]() ,1×
,1× ![]() ),
),
∵矩形AnOCnBn的对角线交点(﹣2× ![]() ×
× ![]() ,1×
,1× ![]() ×
× ![]() ),即(﹣
),即(﹣ ![]() ,
, ![]() ),
),
故答案为:(﹣ ![]() ,
, ![]() ).
).
根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k,即可求得Bn的坐标,然后根据矩形的性质即可求得对角线交点的坐标.本题考查的是矩形的性质、位似变换的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.


科目:初中数学 来源: 题型:
【题目】如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是( )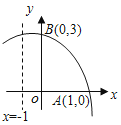
A.顶点坐标为(-1,4)
B.函数的解析式为y=-x2-2x+3
C.当x<0时,y随x的增大而增大
D.抛物线与x轴的另一个交点是(-3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=kx的图象经过点P(1,2),如图所示.
(1)求这个正比例函数的解析式;
(2)将这个正比例函数的图象向右平移4个单位长度,求出平移后的直线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县各中小学校积极组织学生开展课外阅读活动,为了解某校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t〈2,2≤t〈3,3≤t〈4,t≥4分为四个等级,并分别用A、B、C、D表示.根据调查结果统计数据绘制成如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
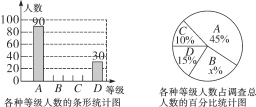
(1)求这次抽查的学生总数是多少人,并求出x的值;
(2)将不完整的条形统计图补充完整;
(3)若该校共有学生3600人,试估计每周课外阅读时间量满足2≤t〈4的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线OC,将一块直角三角板的直角顶点放在O处(注:∠DOE=90°).



(1)如图①,若直角三角板DOE的一边OD放在射线OB上,且∠BOC=60°,求∠COE的度数;
(2)如图②,将三板DOE绕O逆时针转动到某个位置时,若恰好满足5∠COD=∠AOE,且∠BOC=60°,求∠BOD的度数;
(3)如图③,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有黑、白小球各两个,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球后,放回并摇匀,再随机摸出一个小球,则两次摸出的小球都是白球的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com