
【题目】用适当的方法解下列方程.
(1)(2x+3)2-16=0;
(2)(x-2)2-3x(x-2)=0.
(3)x2+4x=2
(4)x(x+4)=8x+12
【答案】(1)x1=![]() , x2= -
, x2= -![]() ;(2)x1=2, x2=-1;(3)x1=-2+
;(2)x1=2, x2=-1;(3)x1=-2+![]() ,x2=-2-
,x2=-2-![]() .(4)x1=6, x2=-2
.(4)x1=6, x2=-2
【解析】
(1)方程运用因式分解法求解即可;
(2)方程先提取公因式(x-2)后化成两个一元一次方程后求解即可;
(3)运用配方法求解即可;
(4)先把方程转化为一般形式后,再运用因式分解法求解即可.
(1)(2x+3)2-16=0;
(2x+3+4)(2x+3-4)=0,
2x+7=0,2x-1=0,
∴x1=![]() , x2= -
, x2= -![]() ;
;
(2)(x-2)2-3x(x-2)=0.
(x-2)(x-2-3x)=0,
x-2=0;-2x-2=0,
∴x1=2, x2=-1;
(3)x2+4x=2
x2+4x+4=2+4
(x+2)2=6,
x+2=±![]()
∴x1=-2+![]() ,x2=-2-
,x2=-2-![]() ;
;
(4)x(x+4)=8x+12
x2-4x-12=0
(x-6)(x+2)=0
x-6=0,x+2=0,
∴x1=6, x2=-2


科目:初中数学 来源: 题型:
【题目】在2020年元月的日历表中,某一天对应的号数的上、下、左、右四个数的和为![]() .
.
(1)如果某一天是![]() 号,请用含
号,请用含 ![]() 的代数式把
的代数式把![]() 表示出来;
表示出来;
(2)![]() 的值可能是96吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由;
的值可能是96吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由;
(3)![]() 的值可能是28吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由.
的值可能是28吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由.
星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)求△DOC的面积.
(3)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )

A.AE=BEB.CE=![]() ABC.∠CEB=2∠AD.AC=
ABC.∠CEB=2∠AD.AC=![]() AB
AB
查看答案和解析>>
科目:初中数学 来源: 题型:
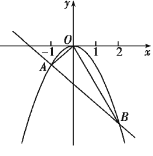
【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A.B两点,如图所示,其中A(-1,-1).
(1)求二次函数和一次函数的解析式;
(2)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=![]() x2﹣
x2﹣![]() x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D
x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D

(1)求出点A,B,D的坐标;
(2)如图1,若线段OB在x轴上移动,且点O,B移动后的对应点为O′,B′.首尾顺次连接点O′、B′、D、C构成四边形O′B′DC,请求出四边形O′B′DC的周长最小值.
(3)如图2,若点M是抛物线上一点,点N在y轴上,连接CM、MN.当△CMN是以MN为直角边的等腰直角三角形时,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组几名同学到商场调查发现,一种纯牛奶进价为每箱40元,厂家要求售价在40~70元之间,若以每箱70元销售平均每天销售30箱,价格每降低1元平均每天可多销售3箱.
(1)现该商场要保证每天盈利900元,同时又要使顾客得到实惠,那么每箱售价为多少元?
(2)若每天盈利为W元,请利用配方法直接写出每箱售价为多少元时,每天盈利最多.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com