
分析 设方程x2-pqx+p+q=0的整数根为x1,x2,根据根与系数的关系得到x1+x2=pq,x1x2=p+q,推出x1,x2同号,x1,x2都大于0,于是得到p+q+1≥pq (p-1)(q-1)≤2,得到方程p-1=1 q-1=2 或p-1=1 q-1=1于是得到结论.
解答 解:设方程x2-pqx+p+q=0的整数根为x1,x2,
∴x1+x2=pq,x1x2=p+q,
∴x1,x2同号,x1,x2都大于0,而两个正整数的乘积+1≥两个正整数的和,
∴p+q+1≥pq,(p-1)(q-1)≤2,
∴p-1=1,q-1=2 或p-1=1,q-1=1,
∴p=2,q=3或 p=2,q=2或p=3,q=2.
点评 本题考查了根与系数的关系,根的判别式.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
上面的结论反过来也成立;


科目:初中数学 来源: 题型:选择题
| A. | 买一张电影票,座位号是奇数 | |
| B. | 从一个只装有红球的袋子里摸出白球 | |
| C. | 三角形两边之和大于第三边 | |
| D. | 明天会下雨 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
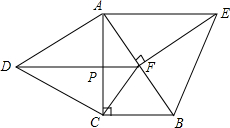 如图,分别以Rt△ABC的直角边AC及斜边AB向形外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF、CF.
如图,分别以Rt△ABC的直角边AC及斜边AB向形外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF、CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图矩形ABCD中,点E在BC上,且AE=EC,试分别在下列两个图中按要求使用无刻度的直尺画图(保留作图痕迹).
如图矩形ABCD中,点E在BC上,且AE=EC,试分别在下列两个图中按要求使用无刻度的直尺画图(保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
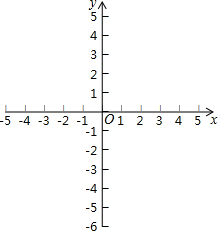 已知:二次函数y=-x2+bx+c的图象过点A(-1,0)和C(0,2).
已知:二次函数y=-x2+bx+c的图象过点A(-1,0)和C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3+6ab2-5a2 | B. | a3-6ab2-5a2 | C. | a3-5a2 | D. | a2+6ab-5a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -($\sqrt{6}$)2=-6 | B. | ($\sqrt{3}$)2=9 | C. | ($\sqrt{16}$)2=±16 | D. | -(-$\sqrt{\frac{16}{25}}$)2=$\frac{16}{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com