
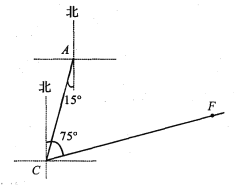
【题目】高考英语听力测试期间,需要杜绝考点周围的噪音,如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点突发火灾,消防队必须立即赶往救火,已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?说明理由.(![]() 取1.732)
取1.732)
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上的中线,
上的中线,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,![]() ,垂足为
,垂足为![]() .
.
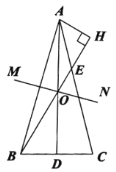
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上的一点,且
上的一点,且![]() ,若
,若![]() ,请你直接写出
,请你直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种泰山旅游纪念品,4月份的营业额为2000元,为扩大销售量,5月份该商店对这种纪念品打9折销售,结果销售量增加20件,营业额增加700元.
(1)求该种纪念品4月份的销售价格;
(2)若4月份销售这种纪念品获利800元,5月份销售这种纪念品获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
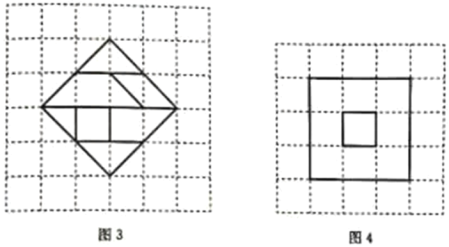
【题目】我们熟知的七巧板,是由宋代黄伯思设计的“燕几图”(“燕几”就是“宴几”,也就是宴请宾客的案几)演变而来.到了明代,严澄将“燕几图”里的方形案几改为三角形,发明了“蝶翅几”.而到了清代初期,在“燕几图”和“蝶翅几”的基础上,兼有三角形、正方形和平行四边形,能拼出更加生动、多样图案的七巧板就问世了(如图1网格中所示)
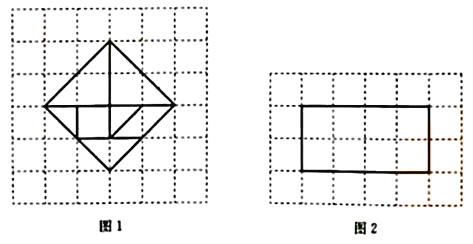
(1)若正方形网格的边长为1,则图1中七巧板的七块拼板的总面积为_____________
(2)使用图1中的七巧板可以拼出一个轮廓如图2所示的长方形,请在图2中画出拼图方法(要求:画出各块拼板的轮廓)
(3)随着七巧板的发展,出现了一些形式不同的七巧板,如图3所示的是另一种七巧板.利用图3中的七巧板可以拼出一个轮廓如图4所示的图形;大正方形的中间去掉一个小正方形,请在图4中画出拼图的方法(要求:画出各块拼板的轮廓)
查看答案和解析>>
科目:初中数学 来源: 题型:
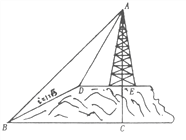
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为![]() ,在山坡的坡顶D处测得铁架顶端A的仰角为
,在山坡的坡顶D处测得铁架顶端A的仰角为![]() ,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O是直线AB上一点,OD是∠AOC的平分线,∠COD与∠COE互余
求证:∠AOE与∠COE互补.

请将下面的证明过程补充完整:
证明:∵O是直线AB上一点
∴∠AOB=180°
∵∠COD与∠COE互余
∴∠COD+∠COE=90°
∴∠AOD+∠BOE=_________°
∵OD是∠AOC的平分线
∴∠AOD=∠________(理由:_______________)
∴∠BOE=∠COE(理由:________________)
∵∠AOE+∠BOE=180°
∴∠AOE+∠COE=180°
∴∠AOE与∠COE互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com