解:(1)第1组3=2×1+1,
第2组5=2×2+1,
第3组7=2×3+1,
…
第n组有2n+1粒,
所以第100组应该有种子2×100+1=201粒.
(2)由a
1=
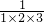
+

=
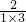
=

,
a
2=
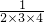
+

=
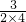
=

,
a
3=
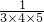
+

=
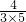
=

,
…
所以a
99=
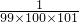
+

=
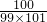
=

;
(3)第1个图案由4=4×1-(1-1)=3+1个基础图形组成,
第2个图案由7=4×2-(2-1)=3×2+1个基础图形组成,
第3个图案由10=4×3-(3-1)=3×3+1个基础图形组成,
…,
那么第101个图案中由3×101+1=304个基础图形组成;
(4)把

,

,

…代入得:
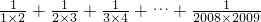
=1-

+

-

+

-

+…+

-

=1-

=

.
分析:(1)第1组取3粒,第2组取5粒,第3组取7粒…第n组取(2n-1)粒解决问题;
(2)所有第一个加数分子是1,分母是三个连续自然数的乘积,第二个加数分子是1,分母是三个连续自然数中间的数,和的分母是三个连续自℃然数两端数的乘积,分子是三个连续自然数中间的数,因此可求得a
99.
(3)第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,第3个图案由10个基础图形组成,…,第n个图案由(3n+1)个基础图形组成,由此解决问题;
(4)由

,

,

,…

=
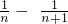
,代入可解决问题.
点评:抓住式子的变化规律或数的变化规律,就可以解决问题.

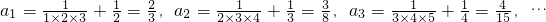 ,依据上述规律,则a99=______;
,依据上述规律,则a99=______;
 ,
, ,
, ,…,根据观察计算:
,…,根据观察计算: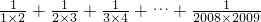 .
.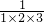 +
+ =
=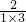 =
= ,
,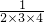 +
+ =
=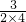 =
= ,
,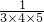 +
+ =
=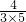 =
= ,
,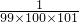 +
+ =
=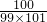 =
= ;
; ,
, ,
, …代入得:
…代入得: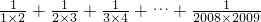
 +
+ -
- +
+ -
- +…+
+…+ -
-

 .
. ,
, ,
, ,…
,… =
=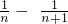 ,代入可解决问题.
,代入可解决问题.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案