
【题目】(2017四川省眉山市)如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G.
(1)求证:BG=DE;
(2)若点G为CD的中点,求![]() 的值.
的值.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题(1)由于BF⊥DE,所以∠GFD=90°,从而可知∠CBG=∠CDE,根据全等三角形的判定即可证明△BCG≌△DCE,从而可知BG=DE;
(2)设CG=1,从而知CG=CE=1,由勾股定理可知:DE=BG=![]() ,由易证△ABH∽△CGH,所以
,由易证△ABH∽△CGH,所以![]() =2,从而可求出HG的长度,进而求出
=2,从而可求出HG的长度,进而求出![]() 的值.
的值.
试题解析:(1)∵BF⊥DE,∴∠GFD=90°,∵∠BCG=90°,∠BGC=∠DGF,∴∠CBG=∠CDE,在△BCG与△DCE中,∵∠CBG=∠CDE,BC=CD,∠BCG=∠DCE,∴△BCG≌△DCE(ASA),∴BG=DE;
(2)设CG=1,∵G为CD的中点,∴GD=CG=1,由(1)可知:△BCG≌△DCE(ASA),∴CG=CE=1,∴由勾股定理可知:DE=BG=![]() ,∵sin∠CDE=
,∵sin∠CDE=![]() ,∴GF=
,∴GF=![]() ,∵AB∥CG,∴△ABH∽△CGH,∴
,∵AB∥CG,∴△ABH∽△CGH,∴![]() ,∴BH=
,∴BH=![]() ,GH=
,GH=![]() ,∴
,∴![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
(1)求抛物线的解析式;
(2)连接BD,点P在抛物线的对称轴上,以Q为平面内一点,四边形PBQD能否成为矩形?若能,请求出点P的坐标;若不能,请说明理由;
(3)在抛物线上有一点M,过点M、A的直线MA交y轴于点C,连接BC,若∠MBO=∠BCO,请直接写出点M的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知△ABC顶点坐标分别为A(0,3),B(1,1),C(﹣3,﹣1),△DEF与△ABC关于y轴对称,且A,B,C依次对应D,E,F,
(1)请写出D,E,F的坐标.
(2)在平面直角坐标系中画出△ABC和△DEF.
(3)经过计算△DEF各边长度,发现DE、EF、FD满足什么关系式,写出关系式.
(4)求△DEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
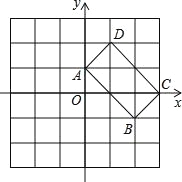
【题目】如图,在 6×6 的网格中,四边形 ABCD 的顶点都在格点上,每个格子都是边长为 1 的正方形,建立如图所示的平面直角坐标系.
(1)画出四边形 ABCD 关于 y 轴对称和四边形 A′B′C′D′(点 A、B、C、D的对称点分别是点 A′B′C′D′.
(2)求 A、B′、B、C 四点组成和四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知双曲线y=![]() (x<0)和y=
(x<0)和y=![]() (x>0),直线OA与双曲线y=
(x>0),直线OA与双曲线y=![]() 交于点A,将直线OA向下平移与双曲线y=
交于点A,将直线OA向下平移与双曲线y=![]() 交于点B,与y轴交于点P,与双曲线y=
交于点B,与y轴交于点P,与双曲线y=![]() 交于点C,S△ABC=6,
交于点C,S△ABC=6,![]() =
=![]() ,则k=( )
,则k=( )

A. ﹣6 B. ﹣4 C. 6 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)小龙一共抽取了 名学生.
(2)补全条形统计图;
(3)求“其他”部分对应的扇形圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)分别写出以下顶点的坐标:A( , );B( , ) ;C( , ).
(2)顶点A关于x轴对称的点A′的坐标( , ),顶点C关于y轴对称的点C′的坐标( , ).
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
(1)在图中标示出旋转中心P,并写出它的坐标;
(2)以原点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2,在图中画出△A2B2C2,并写出C2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com