
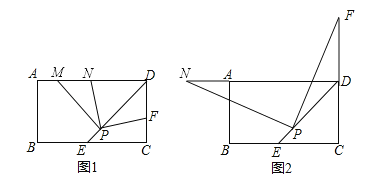
°æƒø°øæÿ–ŒABCD÷–£¨DE∆Ω∑÷°œADCΩªBC±þ”⁄µ„E£¨PŒ™DE…œµƒ“ªµ„£®PE£ºPD£©£¨PM°ÕPD£¨PMΩªAD±þ”⁄µ„M£Æ
£®1£©»Ùµ„F «±þCD…œ“ªµ„£¨¬˙◊„PF°ÕPN£¨«“µ„NŒª”⁄AD±þ…œ£¨»ÁÕº1À˘ æ£Æ
«Û÷§£∫¢ŸPN=PF£ª¢⁄DF+DN=![]() DP£ª
DP£ª
£®2£©»ÁÕº2À˘ 棨µ±µ„F‘⁄CD±þµƒ—”≥§œþ…œ ±£¨»‘»ª¬˙◊„PF°ÕPN£¨¥À ±µ„NŒª”⁄DA±þµƒ—”≥§œþ…œ£¨»ÁÕº2À˘ 棪 ‘Œ DF£¨DN£¨DP”–‘ı—˘µƒ ˝¡øπÿœµ£¨≤¢º”“‘÷§√˜£Æ
°æ¥∞∏°ø£®1£©÷§√˜º˚Ω‚Œˆ£®2£©![]()
°æΩ‚Œˆ°ø∑÷Œˆ£∫£®1£©¢Ÿ¿˚”√æÿ–Œµƒ–‘÷ £¨Ω·∫œ“—÷™Ãıº˛ø…÷§°˜PMN°’°˜PDF£¨‘Úø…÷§µ√Ω·¬€£ª¢⁄”…π¥π…∂®¿Ìø…«Ûµ√DM=![]() DP£¨¿˚”√¢Ÿø…«Ûµ√MN=DF£¨‘Úø…÷§µ√Ω·¬€£ª
DP£¨¿˚”√¢Ÿø…«Ûµ√MN=DF£¨‘Úø…÷§µ√Ω·¬€£ª
£®2£©π˝µ„P◊˜PM1°ÕPD£¨PM1ΩªAD±þ”⁄µ„M1£¨‘Úø…÷§µ√°˜PM1N°’°˜PDF£¨‘Úø…÷§µ√M1N=DF£¨Õ¨£®1£©¢⁄µƒ∑Ω∑®ø…÷§µ√Ω·¬€£Æ
œÍΩ‚£∫£®1£©¢Ÿ°þÀƒ±þ–ŒABCD «æÿ–Œ£¨°ý°œADC=90°„£Æ
”÷°þDE∆Ω∑÷°œADC£¨°ý°œADE=°œEDC=45°„£ª
°þPM°ÕPD£¨°œDMP=45°„£¨°ýDP=MP£Æ
°þPM°ÕPD£¨PF°ÕPN£¨°ý°œMPN+°œNPD=°œNPD+°œDPF=90°„£¨°ý°œMPN=°œDPF£Æ
‘⁄°˜PMN∫Õ°˜PDF÷–£¨°þ 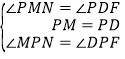 £¨
£¨
°ý°˜PMN°’°˜PDF£®ASA£©£¨°ýPN=PF£¨MN=DF£ª
¢⁄°þPM°ÕPD£¨DP=MP£¨°ýDM2=DP2+MP2=2DP2£¨°ýDM=![]() DP£Æ
DP£Æ
°þ”÷°þDM=DN+MN£¨«“”…¢Ÿø…µ√MN=DF£¨°ýDM=DN+DF£¨°ýDF+DN=![]() DP£ª
DP£ª
£®2£©![]() £Æ¿Ì”…»Áœ¬£∫
£Æ¿Ì”…»Áœ¬£∫
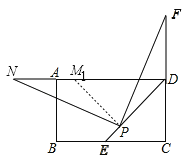
π˝µ„P◊˜PM1°ÕPD£¨PM1ΩªAD±þ”⁄µ„M1£¨»ÁÕº£¨
°þÀƒ±þ–ŒABCD «æÿ–Œ£¨°ý°œADC=90°„£Æ
”÷°þDE∆Ω∑÷°œADC£¨°ý°œADE=°œEDC=45°„£ª
°þPM1°ÕPD£¨°œDM1P=45°„£¨°ýDP=M1P£¨°ý°œPDF=°œPM1N=135°„£¨Õ¨£®1£©ø…÷™°œM1PN=°œDPF£Æ‘⁄°˜PM1N∫Õ°˜PDF÷–£¨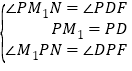 £¨
£¨
°ý°˜PM1N°’°˜PDF£®ASA£©£¨°ýM1N=DF£¨”…π¥π…∂®¿Ìø…µ√£∫![]() =DP2+M1P2=2DP2£¨°ýDM1
=DP2+M1P2=2DP2£¨°ýDM1![]() DP£Æ
DP£Æ
°þDM1=DN©ÅM1N£¨M1N=DF£¨°ýDM1=DN©ÅDF![]() DP£Æ
DP£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
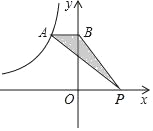
°æƒø°ø»ÁÕºÀ˘ 棨A «∑¥±»¿˝∫Ø ˝ÕºœÛ…œ“ªµ„£¨π˝µ„A◊˜AB°Õy÷·”⁄µ„B£¨µ„P‘⁄x÷·…œ£¨°˜ABPµƒ√ʪ˝Œ™4£¨‘Ú’‚∏ˆ∑¥±»¿˝∫Ø ˝µƒΩ‚Œˆ ΩŒ™_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ»±þ°˜ABCµƒ±þ≥§Œ™3cm£¨∂ص„P¥”µ„A≥ˆ∑¢£¨“‘√ø√Î1cmµƒÀŸ∂»£¨—ÿA°˙B°˙Cµƒ∑ΩœÚ‘À∂Ø£¨µΩ¥Ôµ„C ±Õ£÷π£¨…Ë‘À∂Ø ±º‰Œ™x(s)£¨y£ΩPC2£¨‘Úyπÿ”⁄xµƒ∫Ø ˝µƒÕºœÒ¥Û÷¬Œ™ £® £©
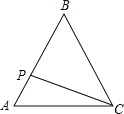
A. 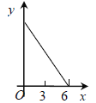 B.
B. 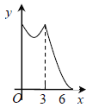 C.
C. 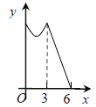 D.
D. 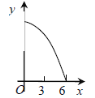
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
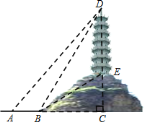
°æƒø°ø»ÁÕº£¨–°√˜Œ™¡À≤‚¡ø–°…Ω∂•µƒÀ˛∏þ£¨À˚‘⁄![]() ¥¶≤‚µ√À˛º‚
¥¶≤‚µ√À˛º‚![]() µƒ—ˆΩ«Œ™
µƒ—ˆΩ«Œ™![]() £¨‘Ÿ—ÿ
£¨‘Ÿ—ÿ![]() ∑ΩœÚ«∞Ω¯
∑ΩœÚ«∞Ω¯![]() µΩ¥Ô…ΩΩ≈
µΩ¥Ô…ΩΩ≈![]() ¥¶£¨≤‚µ√À˛º‚
¥¶£¨≤‚µ√À˛º‚![]() µƒ—ˆΩ«Œ™
µƒ—ˆΩ«Œ™![]() £¨…Ω∆¬
£¨…Ω∆¬![]() µƒ∆¬∂»
µƒ∆¬∂»![]() £¨«ÛÀ˛∏þ£Æ£®æ´»∑µΩ
£¨«ÛÀ˛∏þ£Æ£®æ´»∑µΩ![]() £¨
£¨![]() £©
£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“ª¥Œ∫Ø ˝y=kx+b£®k°¢bŒ™≥£ ˝£¨k°Ÿ0£©µƒÕºœÛ”Îx÷·°¢y÷·∑÷±Ωª”⁄A°¢B¡Ωµ„£¨«“”Î∑¥±»¿˝∫Ø ˝y=![]() £®nŒ™≥£ ˝£¨«“n°Ÿ0£©µƒÕºœÛ‘⁄µ⁄∂˛œÛœÞΩª”⁄µ„C£ÆCD°Õx÷·£¨¥π◊„Œ™D£¨»ÙOB=2OA=3OD=12£Æ
£®nŒ™≥£ ˝£¨«“n°Ÿ0£©µƒÕºœÛ‘⁄µ⁄∂˛œÛœÞΩª”⁄µ„C£ÆCD°Õx÷·£¨¥π◊„Œ™D£¨»ÙOB=2OA=3OD=12£Æ
£®1£©«Û“ª¥Œ∫Ø ˝”Î∑¥±»¿˝∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©º«¡Ω∫Ø ˝ÕºœÛµƒ¡Ì“ª∏ˆΩªµ„Œ™E£¨«Û°˜CDEµƒ√ʪ˝£ª
£®3£©÷±Ω”–¥≥ˆ≤ªµ» Ωkx+b°Ð![]() µƒΩ‚ºØ£Æ
µƒΩ‚ºØ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
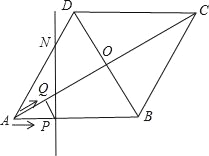
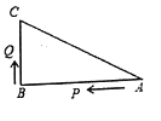
°æƒø°ø»ÁÕº£¨¡‚–ŒABCDµƒ±þ≥§Œ™20cm£¨°œABC£Ω120°„£Æ∂ص„P°¢QÕ¨ ±¥”µ„A≥ˆ∑¢£¨∆‰÷–P“‘4cm/sµƒÀŸ∂»£¨—ÿA°˙B°˙Cµƒ¬∑œþœÚµ„C‘À∂Ø£ªQ“‘2![]() cm/sµƒÀŸ∂»£¨—ÿA°˙Cµƒ¬∑œþœÚµ„C‘À∂أƵ±P°¢QµΩ¥Ô÷’µ„C ±£¨’˚∏ˆ‘À∂ØÀÊ÷ÆΩ· ¯£¨…Ë‘À∂Ø ±º‰Œ™t√ΣÆ
cm/sµƒÀŸ∂»£¨—ÿA°˙Cµƒ¬∑œþœÚµ„C‘À∂أƵ±P°¢QµΩ¥Ô÷’µ„C ±£¨’˚∏ˆ‘À∂ØÀÊ÷ÆΩ· ¯£¨…Ë‘À∂Ø ±º‰Œ™t√ΣÆ
£®1£©‘⁄µ„P°¢Q‘À∂Øπ˝≥Ã÷–£¨«Î≈–∂œPQ”Î∂‘Ω«œþACµƒŒª÷√πÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
£®2£©»Ùµ„Qπÿ”⁄¡‚–ŒABCDµƒ∂‘Ω«œþΩªµ„Oµƒ∂‘≥∆µ„Œ™M£¨π˝µ„P«“¥π÷±”⁄ABµƒ÷±œþlΩª¡‚–ŒABCDµƒ±þAD£®ªÚCD£©”⁄µ„N£Æ
¢Ÿµ±tŒ™∫Œ÷µ ±£¨µ„P°¢M°¢N‘⁄“ª÷±œþ…œ£ø
¢⁄µ±µ„P°¢M°¢N≤ª‘⁄“ª÷±œþ…œ ±£¨ «∑ҥʑ⁄’‚—˘µƒt£¨ πµ√°˜PMN «“‘PNŒ™“ª÷±Ω«±þµƒ÷±Ω«»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆÀ˘”–∑˚∫œÃıº˛µƒtµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨“—÷™![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() °¢
°¢![]() «
«![]() µƒ±þ…œµƒ¡Ω∏ˆ∂ص„£¨∆‰÷–µ„
µƒ±þ…œµƒ¡Ω∏ˆ∂ص„£¨∆‰÷–µ„![]() ¥”µ„
¥”µ„![]() ø™ º—ÿ
ø™ º—ÿ![]() ∑ΩœÚ‘À∂Ø£¨«“ÀŸ∂»Œ™√ø√Î
∑ΩœÚ‘À∂Ø£¨«“ÀŸ∂»Œ™√ø√Î![]() £¨µ„
£¨µ„![]() ¥”µ„
¥”µ„![]() ø™ º—ÿ
ø™ º—ÿ![]() ∑ΩœÚ‘À∂Ø£¨«“ÀŸ∂»Œ™√ø√Î
∑ΩœÚ‘À∂Ø£¨«“ÀŸ∂»Œ™√ø√Î![]() £¨À¸√«Õ¨ ±≥ˆ∑¢£¨…Ë≥ˆ∑¢µƒ ±º‰Œ™
£¨À¸√«Õ¨ ±≥ˆ∑¢£¨…Ë≥ˆ∑¢µƒ ±º‰Œ™![]() £Æ
£Æ
£®1£©‘Ú![]() ____________
____________![]() £ª
£ª
£®2£©µ±![]() Œ™∫Œ÷µ ±£¨µ„
Œ™∫Œ÷µ ±£¨µ„![]() ‘⁄±þ
‘⁄±þ![]() µƒ¥π÷±∆Ω∑÷œþ…œ£ø¥À ±
µƒ¥π÷±∆Ω∑÷œþ…œ£ø¥À ±![]() _________?
_________?
£®3£©µ±µ„![]() ‘⁄±þ
‘⁄±þ![]() …œ‘À∂Ø ±£¨÷±Ω”–¥≥ˆ π
…œ‘À∂Ø ±£¨÷±Ω”–¥≥ˆ π![]() ≥…Œ™µ»—¸»˝Ω«–Œµƒ‘À∂Ø ±º‰£Æ
≥…Œ™µ»—¸»˝Ω«–Œµƒ‘À∂Ø ±º‰£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº÷–£¨AE°ÕAB«“AE£ΩAB£¨BC°ÕCD«“BC£ΩCD£¨»Ùµ„E°¢B°¢DµΩ÷±œþACµƒæý¿Î∑÷±Œ™6°¢3°¢2£¨‘ÚÕº÷– µœþÀ˘Œß≥…µƒ“ı”∞≤ø∑÷√ʪ˝S «( )
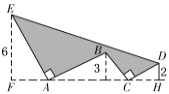
A.50B.44C.38D.32
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ§≥ßΩ”µΩ∂©µ•…˙≤˙»ÁÕºÀ˘ 浃«…øÀ¡¶∞¸◊∞∫–◊”£¨√ø∏ˆ∫–◊””…3∏ˆ≥§∑Ω–Œ≤ý√Ê∫Õ2∏ˆ’˝»˝Ω«–Œµ◊√Ê◊È≥…£¨≤÷ø‚”–º◊°¢““¡Ω÷÷πÊ∏Òµƒ÷Ω∞Âπ≤2600’≈£¨∆‰÷–º◊÷÷πÊ∏Òµƒ÷Ω∞Â∏’∫√ø…“‘≤√≥ˆ4∏ˆ≤ý√Ê£®»ÁÕº¢Ÿ£©£¨““÷÷πÊ∏Òµƒ÷Ω∞Âø…“‘≤√≥ˆ3∏ˆµ◊√Ê∫Õ2∏ˆ≤ý√Ê£®»ÁÕº¢⁄£©£¨≤√ºÙ∫Û±þΩ«¡œ£®Õº÷–“ı”∞≤ø∑÷£©≤ª‘Ÿ¿˚”√£Æ
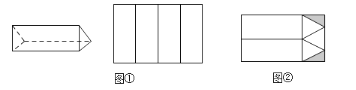
£®1£©»Ù≤√ºÙ≥ˆµƒ≤ý√Ê∫Õµ◊√Ê«°∫√»´≤ø”√ÕÍ£¨Œ ¡Ω÷÷πÊ∏Òµƒ÷Ω∞Â∏˜”–∂ý…Ÿ’≈£ø
£®2£©“ªπ≤ƒÐ…˙≤˙∂ý…Ÿ∏ˆ«…øÀ¡¶∞¸◊∞∫–£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com