
【题目】如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.
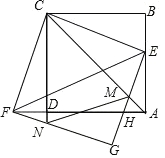
(1)证明:点A、D、F在同一条直线上;
(2)随着点E的移动,线段DH是否有最小值?若有,求出最小值;若没有,请说明理由;
(3)连结EF、MN,当MN∥EF时,求AE的长.
【答案】(1)见解析;(2)有最小值,DH的最小值为![]() ;(3)AE= 2
;(3)AE= 2![]() .
.
【解析】
(1)要证明点A、D、F在同一条直线上,只需证明∠CDF+∠CDA=180°即可.根据题中的已知条件很容易证明△DCF≌△BCE,则∠CDF=∠B=90°,结论可证.
(2)设AE=x,DH=y,通过已知条件证明△ECB∽△HEA,利用相似三角形的性质可知![]() ,即可得到一个y与x的二次函数,根据二次函数的最值可求出线段DH的最小值.
,即可得到一个y与x的二次函数,根据二次函数的最值可求出线段DH的最小值.
(3)利用矩形的性质及平行线的性质可证明△CFN≌△CEM,进而推出∠FCN=∠ECM=∠BCE=22.5°. 在BC上取一点K,使得KC=KE,则△BKE是等腰直角三角形,设BE=BK=a,则KC=KE=![]() a,利用
a,利用![]() 求出a的值,从而利用
求出a的值,从而利用![]() 即可求AE的长.
即可求AE的长.
(1)证明:∵四边形ABCD是正方形,
∴CD=CB,∠BCD=∠B=∠ADC=90°,
∵CE=CF,∠ECF=90°,
∴∠ECF=∠DCB,
∴∠DCF=∠BCE,
∴△DCF≌△BCE,
∴∠CDF=∠B=90°,
∴∠CDF+∠CDA=180°,
∴点A、D、F在同一条直线上.
(2)解:有最小值.
理由:设AE=x,DH=y,则AH=1-y,BE=1-x,
∵四边形CFGE是矩形,
∴∠CEG=90°,
∴∠CEB+∠AEH=90°
CEB+∠ECB=90°,
∴∠ECB=∠AEH,
∵∠B=∠EAH=90°,
∴△ECB∽△HEA,
![]()
即![]()
![]()
∵a=1>0,
∴当![]() 时,y有最小值,最小值为
时,y有最小值,最小值为![]() ,
,
∴DH的最小值为![]() .
.
(3)解:∵四边形CFGE是矩形,CF=CE,
∴四边形CFGE是正方形,
∴GF=GE,∠GFE=∠GEF=45°,
∵NM∥EF,
∴∠GNM=∠GFE,∠GMN=∠GEF,
∴∠GMN=∠GNM,
∴GN=GM,
∴FN=EM,
∵CF=CE,∠CFN=∠CEM,
∴△CFN≌△CEM,
∴∠FCN=∠ECM,
∵∠MCN=45°,
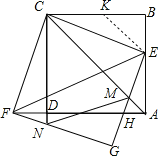
∴∠FCN=∠ECM=∠BCE=22.5°,
在BC上取一点K,使得KC=KE
![]()
![]()
![]()
∴△BKE是等腰直角三角形
设BE=BK=a,则KC=KE=![]() a,
a,
![]()
![]()
![]()


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,等边![]() 的边长为
的边长为![]() ,动点P从点A出发,以每秒
,动点P从点A出发,以每秒![]() 的速度,沿
的速度,沿![]() 的方向运动,到达点C时停止,设运动时间为x(s),则y关于x的函数的图象大致是( )
的方向运动,到达点C时停止,设运动时间为x(s),则y关于x的函数的图象大致是( )

A.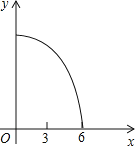 B.
B.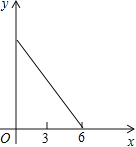 C.
C.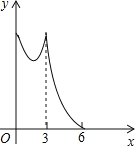 D.
D.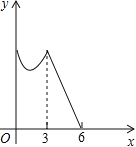
查看答案和解析>>
科目:初中数学 来源: 题型:
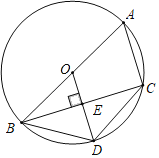
【题目】如图,四边形ABDC内接于⊙O,AB是⊙O的直径,OD⊥BC于点E.
(1)请你写出两个不相同的结论(不添加辅助线);
(2)连接AD,若BE=4,AC=6,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
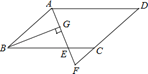
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=![]() ,则△CEF的面积是( )
,则△CEF的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,CD为⊙O的切线,C为切点,过A作CD的垂线,垂足为D.
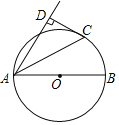
(1)求证:AC平分∠BAD;
(2)若⊙O半径为5,CD=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为A1、A2,图案为“蝴蝶”的卡片记为B)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com