
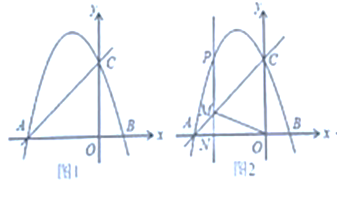
【题目】如图1.抛物线![]() 经过点
经过点![]() 点
点![]() 在抛物线
在抛物线![]() 上,且在
上,且在![]() 轴的上方,点
轴的上方,点![]() 的横坐标记为
的横坐标记为![]() .
.
(1)求抛物线的解析式:
(2)如图2.过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() .交
.交![]() 轴于点
轴于点![]() ,若
,若![]() 平分
平分![]() ,求
,求![]() 的值:
的值:
(3)点![]() 在直线
在直线![]() 上.点
上.点![]() 在
在![]() 轴上,且位于点
轴上,且位于点![]() 的上方,那么在抛物线上是否存在点
的上方,那么在抛物线上是否存在点![]() ,使得以点
,使得以点![]() 为顶点的四边形是菱形?若存在,请直接写出菱形的面积.
为顶点的四边形是菱形?若存在,请直接写出菱形的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]()
【解析】
(1)设抛物线的解析式为![]() ,将点C(0,3)代入即可解答;
,将点C(0,3)代入即可解答;
(2)求出直线AC的解析式为![]() ,设P的横坐标为t,则
,设P的横坐标为t,则![]() ,根据平行线的性质以及角平分线的定义得到
,根据平行线的性质以及角平分线的定义得到![]() ,根据勾股定理列出方程即可求出t的值;
,根据勾股定理列出方程即可求出t的值;
(3)分两种情况:①当CE为对角线时,四边形CPED为菱形,如图3,则点P和点D关于y轴对称;②当CE为菱形的边时,四边形CEPD为菱形,如图4,则PD∥y轴,CD=PD,分别构建方程即可解决问题.
解:(1)∵抛物线![]() 经过点
经过点![]() ,
,
∴设抛物线的解析式为![]() ,
,
把![]() 代入得到
代入得到![]()
![]() 抛物线的解析式为
抛物线的解析式为![]() ,
,
即![]()
(2)如图2中
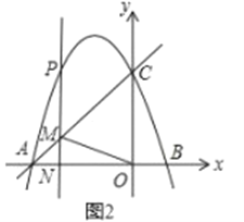
设直线AC的解析式为y=kx+p,将![]() 代入得:
代入得:
![]() ,解得k=
,解得k=![]() ,p=3,
,p=3,
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]() 的横坐标为
的横坐标为![]() ,
,
![]()
![]() 平分
平分![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() 或t=0(舍去)
或t=0(舍去)
![]() 的值为
的值为![]()
(3)设![]() ,
,
①当CE为对角线时,四边形CPED为菱形,如图3,则点P和点D关于y轴对称,
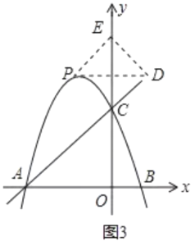
∴点![]() ,
,
将![]() 代入
代入![]() 中得:
中得:
![]() ,
,
解得:![]() (舍去)
(舍去)
此时P(-2,![]() ),
),
∴PD=4,CE=2×(![]() -3)=3
-3)=3
∴菱形的面积=![]() ;
;
②当CE为菱形的边时,四边形CEPD为菱形,如图4,则PD∥y轴,CD=PD,
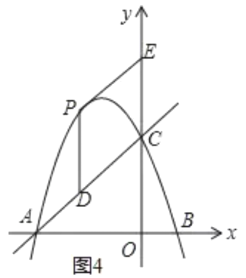
∴![]() ,
,
∴PD=![]()
而![]() ,
,
∴![]() ,
,
∴![]() ,解得:
,解得:![]() (舍去),
(舍去),
∴PD=![]() ,
,
此时菱形的面积=![]() .
.
综上所述,菱形的面积是![]() 或
或![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】如图1,在一张ABCD的纸片中,ABCD的面积为6,DC=3,∠BCD=45°,点P是BD上的一动点(点P与点B,D不重合).现将这张纸片分别沿BD,AP剪成三块,并按图2(注:图2中的①,②是将图1中的①,②翻转背面朝上,再拼接而成的)所示放置
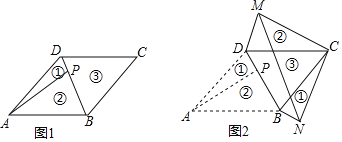
(1)当点P是BD的中点时,求AP的长.
(2)试探究:当点P在BD的什么位置上时,MN的长最小?请求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两盒中分别标注数字2、![]() 、
、![]() 、和
、和![]() 、1、6的3张卡片,这些卡片除数字外都相同,把卡片洗匀后,从甲、乙两盒中各任意抽取1张,并把从甲盒中抽得卡片上的数字作为一个点的横坐标,从乙盒中抽得卡片上的数字作为这个点的纵坐标.
、1、6的3张卡片,这些卡片除数字外都相同,把卡片洗匀后,从甲、乙两盒中各任意抽取1张,并把从甲盒中抽得卡片上的数字作为一个点的横坐标,从乙盒中抽得卡片上的数字作为这个点的纵坐标.
(1)请利用列表或画树状图的方法列出这样的点所有可能的坐标;
(2)计算这些点落在以原点为圆心、3为半径的圆内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某制衣厂某车间计划用10天加工一批出口童装和成人装共360件,该车间的加工能力是:每天能单独加工童装45件或成人装30件。
(1)该车间应安排几天加工童装,几天加工成人装,才能如期完成任务?
(2)若加工童装一件可获利80元, 加工成人装一件可获利120元, 那么该车间加工完这批服装后,共可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:h),随机调査了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
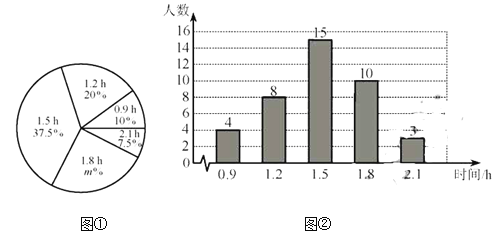
(Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com