
【题目】(10分)为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,m3表示立方米):

请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水4m3,则应收水费_____元;
(2)若该户居民3月份用水am3(其中6m3<a<10m3),则应收水费多少元?(用含a的代数式表示,并化简)
(3)若该户居民4,5两个月共用水15m3,并且4月份用水量不超过6 m3,设4月份用水xm3,求该户居民4,5两个月共交水费多少元?(用含x的代数式表示,并化简)
【答案】(1)8元 ;(2)4a-12;(3)48-2x或68-6x
【解析】试题分析:对于(1),不超过6m3,单价为2元,水费=单价×数量,据此解答;
对于(2),由题意得水费=单价为2元的6m3的水费+单价为4元的超过6m3的水费;
对于(3)应分情况讨论:4月份不超过6m3,5月份10立方米以上;或4月份不超过6m3,5月份在6-10立方米之间.
解:(1)2×4=8(元);
(2)4(a-6)+6×2=4a-12,
所以应收水费为(4a-12)元.
(3)因为5月份用水量超过了4月份,所以4月份用水量少于7.5m3.
①当4月份用水量少于5m3时,则5月份用水量超过10m3,
所以4,5两个月共交水费=2x+8(15-x-10)+4×4+6×2=-6x+68(元);
②当4月份用水量大于或等于5m3但不超过6m3时,则5月份用水量不少于9m3但不超过10m3,
所以4、5两个月共交水费
2x+4(15-x-6)+6×2=-2x+48(元);


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )

A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)如图1,四边形ABCD是正方形,点E、点F分别在边AB和AD上,且AE=AF.此时,线段BE、DF的数量关系是 , 位置关系是 . 请直接写出结论.
(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由.
(3)如图3,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当α=90°时,连接BE、DF,若正方形的边长为1,猜想当AE=时,直线DF垂直平分BE.请写出计算过程.
(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有
①![]() 的算术平方根是5
的算术平方根是5
②关于x的方程m![]() +2x+1=0没有实数根,那么m的取值范围是m>1且m≠0.
+2x+1=0没有实数根,那么m的取值范围是m>1且m≠0.
③一组数据:1,1,3,3的方差是![]() .
.
④已知三角形的两边长分别为3和4,则第三边长c的取值范围是1<c<7.
⑤在平行四边形、线段、角、等边三角形四个图形中,既是轴对称图形又是中心对称图的只有一个.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
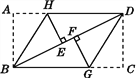
【题目】如图,把一张长方形纸片ABCD按图中的方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.试说明:△BHE≌△DGF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司的电话号码是八位数,这个号码的前四位数字相同,后五位数字是连续减少1的自然数,全部数字之和恰好等于号码的最后两位数,那么,该公司的电话号码是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com