
【题目】某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:
x(天) | 1 | 2 | 3 | … |
m(kg) | 20 | 24 | 28 | … |
(1)请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式
(2)求在销售的第几天时,当天的利润最大,最大利润是多少?
(3)请求出试销的20天中当天的销售利润不低于1680元的天数.
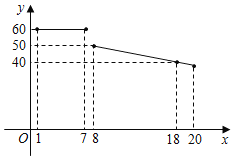
【答案】(1)y=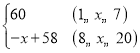 ,m=4x+16(0≤x≤20,且x为整数);(2)在销售的第18天时,当天的利润最大,最大利润是1936元;(3)试销的20天中当天的销售利润不低于1680元的有13天
,m=4x+16(0≤x≤20,且x为整数);(2)在销售的第18天时,当天的利润最大,最大利润是1936元;(3)试销的20天中当天的销售利润不低于1680元的有13天
【解析】
(1)利用待定系数法求解可得;
(2)设当天的总利润为w,分1≤x≤7和8≤x≤20两种情况,根据“总利润=每千克利润×日销售量”列出函数解析式,再依据一次函数和二次函数的性质分别求解可得;
(3)在两种情况下,分别求出w≥1680时对应的x的范围,从而得出答案.
(1)当1≤x≤7时,y=60;
当8≤x≤20时,设y=kx+b,
将(8,50)、(18,40)代入得![]() ,
,
解得![]() ,
,
∴![]() ;
;
综上,y=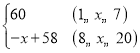
设![]() ,
,
将(1,20)、(2,24)代入得![]() ,
,
解得![]() ,
,
则![]() (0≤x≤20,且x为整数);
(0≤x≤20,且x为整数);
(2)设当天的总利润为w,
当![]() 时,
时,![]() ,
,
则![]() 时,w取得最大值,最大值为1848元;
时,w取得最大值,最大值为1848元;
当![]() 时,
时,![]()
![]()
![]() ,
,
∴当x=18时,w取得最大值,最大利润为1936元;
综上,在销售的第18天时,当天的利润最大,最大利润是1936元;
(3)当![]() 时,
时,![]() ,
,
解得![]() ,
,
∴此时满足条件的天数为第6、7这2天;
当![]() 时,
时,![]() ,
,
解得![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴此时满足条件的天数有11天;
综上,试销的20天中当天的销售利润不低于1680元的有13天.


科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数
的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数![]() (k≠0)图象在第二象限内的交点.
(k≠0)图象在第二象限内的交点.
(1)求点B的坐标及k的值;
(2)试在x轴上确定点C,使AC=AB,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
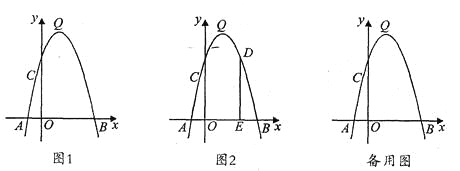
【题目】如图1,抛物线y=-x2+bx+c的顶点为Q,与x轴交于A(-1,0)、B(5,0)两点,与y轴交于点C.
(1)求抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线的对称轴上求一点P,使得△PAC的周长最小,请在图中画出点P的位置,并求点P的坐标;
(3)如图2,若点D是第一象限抛物线上的一个动点,过D作DE⊥x轴,垂足为E.
①有一个同学说:“在第一象限抛物线上的所有点中,抛物线的顶点Q与x轴相距最远,所以当点D运动至点Q时,折线D-E-O的长度最长”,这个同学的说法正确吗?请说明理由.
②若DE与直线BC交于点F.试探究:四边形DCEB能否为平行四边形?若能,请直接写出点D的坐标;若不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
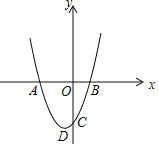
【题目】已知二次函数y=x2+2x﹣3图象的顶点为D,与x轴交于点A、B,与y轴交于点C.
(1)求A、B、C三点的坐标;
(2)当﹣2<x<2时,y的取值范围是 ;
(3)判定△ACD的形状为 三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 为边
为边![]() 和
和![]() 上的动点(不含端点),
上的动点(不含端点),![]() .下列三个结论:①当
.下列三个结论:①当![]() 时,则
时,则![]() ;②
;②![]() ;③
;③![]() 的周长不变,其中正确结论的个数是( )
的周长不变,其中正确结论的个数是( )

A.0B.1
C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
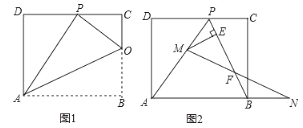
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.
(2)如图2,在(1)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机取出一个小球,记下数字为
,小红在剩下的3个小球中随机取出一个小球,记下数字为![]() 。
。
(1)计算由![]() 、
、![]() 确定的点
确定的点![]() 在函数
在函数![]() 的图象上的概率;
的图象上的概率;
(2)小明和小红约定做一个游戏,其规则为:若![]() 、
、![]() 满足
满足![]() >6则小明胜,若
>6则小明胜,若![]() 、
、![]() 满足
满足![]() <6则小红胜,这个游戏公平吗?说明理由.若不公平,请写出公平的游戏规则.
<6则小红胜,这个游戏公平吗?说明理由.若不公平,请写出公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“永定楼”,作为门头沟区的地标性建筑,因其坐落在永定河畔而得名.为测得其高度,低空无人机在A处,测得楼顶端B的仰角为30°,楼底端C的俯角为45°,此时低空无人机到地面的垂直距离AE为23![]() 米,那么永定楼的高度BC是______米(结果保留根号).
米,那么永定楼的高度BC是______米(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 为弧
为弧![]() 的中点,正方形
的中点,正方形![]() 绕点
绕点![]() 旋转与
旋转与![]() 的两边分别交于
的两边分别交于![]() 、
、![]() (点
(点![]() 、
、![]() 与点
与点![]() 、
、![]() 、
、![]() 均不重合),与
均不重合),与![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)求证:![]() 为等腰直角三角形;
为等腰直角三角形;
(2)求证:![]() ;
;
(3)连接![]() ,试探究:在正方形
,试探究:在正方形![]() 绕点
绕点![]() 旋转的过程中,
旋转的过程中,![]() 的周长是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.
的周长是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com