
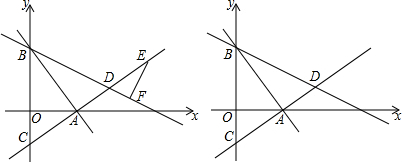
���� ��1�����ۣ�AB��CA�������B��C�������꣬�����ֱ��AB��AC�Ľ���ʽ�����жϣ�
��2�����������ν���x��2$\sqrt{3}$����x��2$\sqrt{3}$���ֱ�Z��Rt��DEF�У���ֱ�������μ��ɣ�
��3���������������ۼ��ɢٵ�ABΪ���ζԽ���ʱ���߶�AB�Ĵ�ֱƽ���ߵĽ���ʽΪy=$\frac{\sqrt{3}}{3}$x+1��ֱ��y=$\frac{\sqrt{3}}{3}$x+1��y��Ľ��㼴Ϊ��Q����ʱQ1��0��1����
�ڵ�ABΪ���εı�ʱ��AB=BP=2$\sqrt{3}$���ɵ�P2��3��3-$\sqrt{3}$����P3��-3��3+$\sqrt{3}$�����������ε����������Q���꼴�ɣ�
��� �⣺��1��AB��AC���������£�
��һԪ���η���x2-2x-3=0��������Ϊ-1��3��
��C��0��-1����B��0��3����
��A��$\sqrt{3}$��0����
��ֱ��AB�Ľ���ʽΪy=-$\sqrt{3}$x+3��ֱ��AC�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x-1��
��-$\sqrt{3}$��$\frac{\sqrt{3}}{3}$=-1��
��AB��AC��
��2����ͼ1�У���DM��BC��M��
��DB=DC��DM��BC��
��BM=CM=2��
��OM=1��D��2$\sqrt{3}$��1����
��tan��OAC=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$��
���CAO=30�㣬��DCB=��OAB=60�㣬
��DC=DB��
���DBC�ǵȱ������Σ�
��CD=BC=4��AC=AD=2��
�ٵ���E�ڵ�D�Ϸ�ʱ����x��2$\sqrt{3}$ʱ��
�ߵ�E�ĺ�����Ϊx��
��AE=$\frac{2\sqrt{3}}{3}$��x-$\sqrt{3}$��=$\frac{2\sqrt{3}}{3}$x-2��DE=AE-AD=$\frac{2\sqrt{3}}{3}$x-4��
�ߡ�EDF=��BDC=60�㣬
��d=EF=DE•cos30��=��$\frac{2\sqrt{3}}{3}$x-4��•$\frac{\sqrt{3}}{2}$=x-2$\sqrt{3}$��
�ڵ���E�ڵ�D�·�ʱ����x��2$\sqrt{3}$ʱ��ͬ���ɵ�d=2$\sqrt{3}$-x��
��������d=$\left\{\begin{array}{l}{x-2\sqrt{3}}&{��x��2\sqrt{3}��}\\{2\sqrt{3}-x}&{��x��2\sqrt{3}��}\end{array}\right.$��
��3����ͼ2�У����ڣ��������£�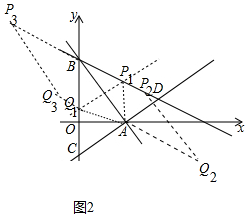
��ABΪ���ζԽ���ʱ���߶�AB�Ĵ�ֱƽ���ߵĽ���ʽΪy=$\frac{\sqrt{3}}{3}$x+1��
ֱ��y=$\frac{\sqrt{3}}{3}$x+1��y��Ľ��㼴Ϊ��Q����ʱQ1��0��1����
��ABΪ���εı�ʱ��AB=BP=2$\sqrt{3}$���ɵ�P2��3��3-$\sqrt{3}$����P3��-3��3+$\sqrt{3}$����
���ı���ABP2Q2���ı���ABP3Q3�����Σ�
��Q2��3+$\sqrt{3}$��-$\sqrt{3}$����Q3��$\sqrt{3}$-3��$\sqrt{3}$����
�������������������ĵ�Q���꣨0��1����3+$\sqrt{3}$��-$\sqrt{3}$����$\sqrt{3}$-3��$\sqrt{3}$����
���� ���⿼���ı����ۺ��⡢һ�κ�������ֱ��λ�ù�ϵ�����ε��ж������ʡ���ֱ�������ε�֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
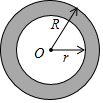 ��ͼ��һ��Բ������Բ����Բ�İ뾶�ֱ���R��r��
��ͼ��һ��Բ������Բ����Բ�İ뾶�ֱ���R��r���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | 0.1$\stackrel{•}{0}$$\stackrel{•}{1}$ | C�� | $\sqrt{4}$ | D�� | $\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3$\sqrt{2}$ | B�� | $\sqrt{32}$ | C�� | $\sqrt{24}$ | D�� | $\frac{1}{\sqrt{8}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1 | B�� | ��9 | C�� | 1��9 | D�� | -1��-9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����6��6�������У�ÿ��С�����εı߳�����1����������Rt��ABC��ʹ��A��C�ڸ���ϣ���ACB=90�㣬AC=4��AB=$\sqrt{29}$��˵����������������BC�ij���
��ͼ����6��6�������У�ÿ��С�����εı߳�����1����������Rt��ABC��ʹ��A��C�ڸ���ϣ���ACB=90�㣬AC=4��AB=$\sqrt{29}$��˵����������������BC�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��������OM��������A��B��C��OA=20��AB=m��BC=n��m��n����|m-6n|=-��10-n��2����P�ӵ�O��������OM������ÿ��1����λ���ٶ������˶�����Q�ӵ�C�������߶�CO�����O�����˶�����O�˶�����Oʱֹͣ�˶���������ͬʱ������
��ͼ��ʾ��������OM��������A��B��C��OA=20��AB=m��BC=n��m��n����|m-6n|=-��10-n��2����P�ӵ�O��������OM������ÿ��1����λ���ٶ������˶�����Q�ӵ�C�������߶�CO�����O�����˶�����O�˶�����Oʱֹͣ�˶���������ͬʱ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ��İ��̣������㹻����Ϊһ�ߣ����ܳ�Ϊ80m��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ���������������������������������ȣ���BC�ij���Ϊxm
Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ��İ��̣������㹻����Ϊһ�ߣ����ܳ�Ϊ80m��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ���������������������������������ȣ���BC�ij���Ϊxm�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com