
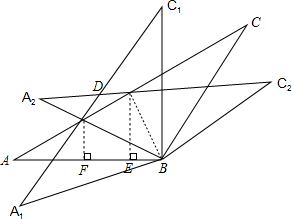
 如图,在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B旋转30°得到△A1BC1,设AC交A1C1于点D,则点D到AB的距离为$\sqrt{3}$-1或1.
如图,在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B旋转30°得到△A1BC1,设AC交A1C1于点D,则点D到AB的距离为$\sqrt{3}$-1或1. 分析 ①如图1,根据旋转的性质得到∠CBC1=30°,A1B=AB=BC=BC1=2,以B为原点,直线AB为x轴,直线BC1为y轴建立平面直角坐标系,根据等腰三角形的性质得到∠BAC=∠C=30°,解直角三角形得到A(-2,0),C1(0,2),A1(-$\sqrt{3}$,-1),C(1,$\sqrt{3}$),求得直线AC的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$,直线A1C1的解析式为y=$\sqrt{3}$x+2,联立方程组即可得到结论;②如图2,根据旋转的性质得到∠CBC1=30°,A1B=AB=BC=BC1=2,根据等腰三角形的性质得到∠A=∠C=∠C1=30°,推出四边形ABC1D是平行四边形,得到四边形ABC1D是菱形,然后解直角三角形即可得到结论.
解答  解:①如图1,∵将△ABC绕点B逆时针旋转30°得到△A1BC1,
解:①如图1,∵将△ABC绕点B逆时针旋转30°得到△A1BC1,
∴∠CBC1=30°,A1B=AB=BC=BC1=2,
∵∠ABC=120°,
∴∠ABC1=90°,
以B为原点,直线AB为x轴,直线BC1为y轴建立平面直角坐标系,
∵AB=BC=2,∠ABC=120°,
∴∠BAC=∠C=30°,
∴A(-2,0),C1(0,2),A1(-$\sqrt{3}$,-1),C(1,$\sqrt{3}$),
∴直线AC的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$,
直线A1C1的解析式为y=$\sqrt{3}$x+2,
解$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x+\frac{2\sqrt{3}}{3}}\\{y=\sqrt{3}x+2}\end{array}\right.$得$\left\{\begin{array}{l}{x=1-\sqrt{3}}\\{y=\sqrt{3}-1}\end{array}\right.$,
∴D(1-$\sqrt{3}$,$\sqrt{3}$-1),
∴点D到AB的距离为$\sqrt{3}$-1;
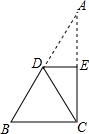
②如图2,∵将△ABC绕点B逆时针旋转30°得到△A1BC1,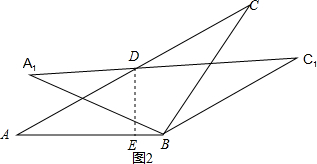
∴∠CBC1=30°,A1B=AB=BC=BC1=2,
∵∠ABC=120°,
∴∠A=∠C=∠C1=30°,
∴∠ABC1=150°,
∴∠ADC1=150°,
∴∠A=∠C1,∠ABC1=∠ADC1,
∴四边形ABC1D是平行四边形,
∵AB=BC1=2,
∴四边形ABC1D是菱形,
∴AD=2,
过D作DE⊥于E,
∵∠A=30°,
∴DE=$\frac{1}{2}$AD=1,
综上所述:点D到AB的距离为:$\sqrt{3}$-1或1,
故答案为:$\sqrt{3}$-1或1.
点评 本题考查了旋转的性质,等腰三角形的性质,直角三角形的性质,求函数的解析式,正确的理解题意是解题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
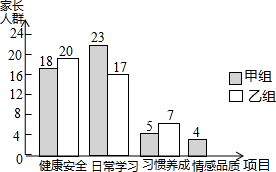 为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.
为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.7×105 | B. | 7×104 | C. | 7×105 | D. | 70×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 67、68 | B. | 67、67 | C. | 68、68 | D. | 68、67 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
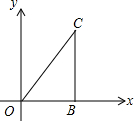 如图所示:在直角坐标系中,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°得到△OB2C2,…如此继续,得到△OB2016C2016则点C2016的坐标是(-2,0).
如图所示:在直角坐标系中,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°得到△OB2C2,…如此继续,得到△OB2016C2016则点C2016的坐标是(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x+19 | B. | 2x-19 | C. | 2x+15 | D. | 2x-15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)解方程组:$\left\{\begin{array}{l}{x-y=2}\\{x-y=y+1}\end{array}\right.$.
(1)解方程组:$\left\{\begin{array}{l}{x-y=2}\\{x-y=y+1}\end{array}\right.$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com