
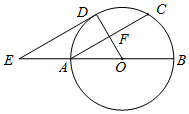
 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.分析 (1)欲证明AC∥DE,只要证明AC⊥OD,ED⊥OD即可.
(2)由△AFO≌△CFD(SAS),推出S△AFO=S△CFD,推出S四边形ACDE=S△ODE,求出△ODE的面积即可.
解答 证明:(1)∵F为弦AC(非直径)的中点,
∴AF=CF,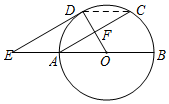
∴OD⊥AC,
∵DE切⊙O于点D,
∴OD⊥DE,
∴AC∥DE.
(2)∵AC∥DE,且OA=AE,
∴F为OD的中点,即OF=FD,又∵AF=CF,
∠AFO=∠CFD,
∴△AFO≌△CFD(SAS),
∴S△AFO=S△CFD,
∴S四边形ACDE=S△ODE
在Rt△ODE中,OD=OA=AE=2,
∴OE=4,
∴DE=$\sqrt{O{E^2}-O{D^2}}=\sqrt{{4^2}-{2^2}}$=2$\sqrt{3}$
∴S四边形ACDE=S△ODE=$\frac{1}{2}$×OD×DE=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$.
点评 本题考查切线的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-6,0),B(-1,1),C(-3,3),将△ABC绕点B顺时针方向旋转90°后得到△A1BC1.
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-6,0),B(-1,1),C(-3,3),将△ABC绕点B顺时针方向旋转90°后得到△A1BC1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品种 | 购买价(元/棵) | 成活率 |
| A | 28 | 90% |
| B | 40 | 95% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
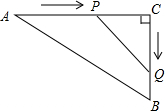 如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )| A. | 5秒 | B. | 20秒 | C. | 5秒或20秒 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com