
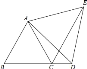
【题目】如图,已知等边△ABC中,点D在BC边的延长线上,CE平分∠ACD,且CE=BD.判断△ADE的形状,并说明理由。
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】小明家准备装修一套新住房,若甲、乙两个装饰公司,合做需6周完成,需工钱5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,需工钱4.8万元,若只选一个公司单独完成,从节约开支角度考虑,小明家是选甲公司、还是乙公司请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)如图1,等边△ABC中,P是AC边上一点,Q是CB延长线上一点,若AP=BQ.则过P作PF∥BC交AB于F,可证△APF是等边三角形,再证△PDF≌QDB可得D是FB的中点.请写出证明过程.
(运用)如图2,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A,C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.

(1)当∠BQD=30°时,求AP的长;
(2)在运动过程中线段ED的长是否发生变化?如果不变,直接写出线段ED的长;如果发生改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班参加一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a满分20分,题b、题c满分均为25分.竞赛结果,每个学生至少答对了一题,三题全答对的有1人,答对其中两道题的有15人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为25,答对题b的人数与答对题c的人数之和为20,在这个班的平均成绩是__分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC,△DEC均为直角三角形,B,C,E三点在一条直线上,过D作DM⊥AC于M.

(1)如图1,若△ABC≌△DEC,且AB=2BC.
①过B作BN⊥AC于N,则线段AN,BN,MN之间的数量关系为: ;(直接写出答案)
②连接ME,求![]() 的值;
的值;
(2)如图2,若AB=CE=DE,DM=2,MC=1,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形![]() 中,
中,![]() ,有一只蚂蚁
,有一只蚂蚁![]() 在点
在点![]() 处开始以每秒1个单位的速度沿
处开始以每秒1个单位的速度沿![]() 边向点
边向点![]() 爬行,另一只蚂蚁
爬行,另一只蚂蚁![]() 从点
从点![]() 以每秒2个单位的速度沿
以每秒2个单位的速度沿![]() 边向点
边向点![]() 爬行,蚂蚁的大小忽略不计,如果
爬行,蚂蚁的大小忽略不计,如果![]() 、
、![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() s.
s.

(1)当![]() 时,求
时,求![]() 的面积;
的面积;
(2)当![]() 时,试说明
时,试说明![]() 是直角二角形;
是直角二角形;
(3)当运动3s时,![]() 点停止运动,
点停止运动,![]() 点以原速立即向
点以原速立即向![]() 点返回,在返回的过程中,是否存在点
点返回,在返回的过程中,是否存在点![]() ,使得
,使得![]() 平分
平分![]() ?若存在,求出点
?若存在,求出点![]() 运动的时间,若不存在请说明理由.
运动的时间,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象 与x轴、y轴分别交于点A,B.
的图象 与x轴、y轴分别交于点A,B.

(1)求点A,B的坐标;
(2)M为ー次函数y=x+3的图象上一点,若 △ABM与△ABO的面积相等,求点M的坐标;
(3)Q为y轴上的一点,若三角形ABQ为等腰三角形 ,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是 ;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从这个袋子中任意摸只球,组成一个两位数,求所组成的两位数是5的倍数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com