
 已知:如图,在Rt△ABC中,∠C=90°,CD为斜边AB上的高.
已知:如图,在Rt△ABC中,∠C=90°,CD为斜边AB上的高. (m-1)=0有两个不相等的实数根,试求m的取值范围;
(m-1)=0有两个不相等的实数根,试求m的取值范围; (m-1)=0有两个不相等的实数根,
(m-1)=0有两个不相等的实数根, (m-1)>0,
(m-1)>0, 且m≠0;
且m≠0;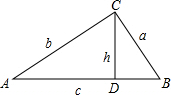 设AC=b,BC=a,AB=c,AB上高CD=h,
设AC=b,BC=a,AB=c,AB上高CD=h, ab=
ab= ch,
ch, ,
, =
= =
= ,
, (m-1)=0,
(m-1)=0, ,sinA•sinB=
,sinA•sinB= ,
, )2+(
)2+( )2=
)2=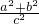 =1,
=1, )2-2×
)2-2× =1,
=1, =0,
=0, •
• =
=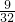 ,
, =
=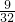 ,
, ;
; •
• =0,
=0, .
. (m-1)>0,求出即可;
(m-1)>0,求出即可; ,sinA•sinB=
,sinA•sinB= ,根据sin2A+sin2B=1推出(
,根据sin2A+sin2B=1推出( )2-2×
)2-2× =1,求出m的值,代入方程即可得出答案.
=1,求出m的值,代入方程即可得出答案.

科目:初中数学 来源: 题型:
 (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.| 3 |
| 5 |
| 14 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com