
【题目】已知点A(a,3),点C(5,c),点B的纵坐标为6且横纵坐标互为相反数,直线AC![]() 轴,直线CB
轴,直线CB![]() 轴:
轴:
(1)写出A、B、C三点坐标;
(2)求△ABC的面积;
(3)若P为线段OB上动点且点P的横、纵坐标互为相反数,当△BCP的面积大于12小于16时,求点P横坐标取值范围.

【答案】(1)A(5,3),B(-6,6),C(5,6);(2)![]() ;(3)点P横坐标取值范围为:-
;(3)点P横坐标取值范围为:-![]() <a<-
<a<-![]() .
.
【解析】
(1)根据题意得出A和C的横坐标相同,B和C的纵坐标相同,得出A(5,3),C(5,6),由角平分线的性质得出B的坐标;
(2)求出BC=5-(-6)=11,即可得出△ABC的面积;
(3)设P的坐标为(a,-a),则△BCP的面积=![]() ×11×(6+a),根据题意得出不等式12<
×11×(6+a),根据题意得出不等式12<![]() ×11×(6+a)<16,解不等式即可.
×11×(6+a)<16,解不等式即可.
解:(1)如图所示:
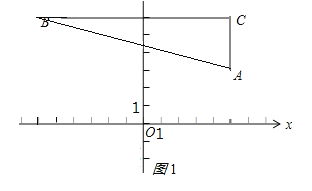
∵AC⊥x轴,CB⊥y轴,
∴A和C的横坐标相同,B和C的纵坐标相同,
∴A(5,3),C(5,6),
∵点B的纵坐标为6且横纵坐标互为相反数,
∴B(-6,6);
(2)∵BC=5-(-6)=11,
∴△ABC的面积=![]() ×11×(6-3)=
×11×(6-3)=![]() ;
;
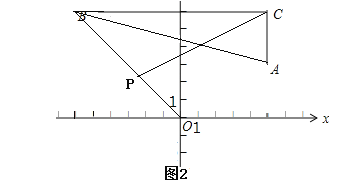
(3)设P的坐标为(a,-a),
则△BCP的面积=![]() ×11×(6+a),
×11×(6+a),
∵△BCP面积大于12小于16,
∴12<![]() ×11×(6+a)<16,
×11×(6+a)<16,
解得:-![]() <a<-
<a<-![]() ;
;
即点P横坐标取值范围为:-![]() <a<-
<a<-![]() .
.
故答案为:(1)A(5,3),B(-6,6),C(5,6);(2)![]() ;(3)点P横坐标取值范围为:-
;(3)点P横坐标取值范围为:-![]() <a<-
<a<-![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上运动,设
上运动,设![]() 长为
长为![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 从小到大变化时,
从小到大变化时,![]() 也随之变化.
也随之变化.

(1)求出![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)完成下面的表格
| 4 | 5 | 6 | 7 |
| 6 |
(3)由表格看出当![]() 每增加
每增加![]() 时,
时,![]() 如何变化?
如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图,在△![]() 中,把
中,把![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称△
时,我们称△![]() 是△
是△![]() 的“旋补三角形”,△
的“旋补三角形”,△![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.
叫做“旋补中心”.
⑴ 特例感知:在如图、如图中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
① 如图,当![]() 为等边三角形时,
为等边三角形时,![]() 与
与![]() 的数量关系为
的数量关系为![]() =
= ![]() ;
;
② 如图,当![]() ,
,![]() 时,则
时,则![]() 长为 .
长为 .
⑵ 精确作图:如图,已知在四边形![]() 内部存在点
内部存在点![]() ,使得
,使得![]() 是
是![]() 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点![]() (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)
⑶ 猜想论证:在如图中,当△![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.
(1)求证:CF为⊙O的切线.
(2)若半径ON⊥AD于点M,CE=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
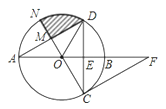
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() (其中k为常数,且
(其中k为常数,且![]() ),则称点
),则称点![]() 为点P的“k属派生点”.
为点P的“k属派生点”.
例如:![]() 的“4属派生点”为
的“4属派生点”为![]() ,即
,即![]() .
.
(1)点![]() 的“2属派生点”
的“2属派生点”![]() 的坐标为________;
的坐标为________;
(2)若点P的“3属派生点”![]() 的坐标为
的坐标为![]() ,求点P的坐标;
,求点P的坐标;
(3)若点P在y轴的正半轴上,点P的“k属派生点”为![]() 点,且点
点,且点![]() 到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在网格坐标系中画出二次函数![]() 的大致图象(注:图中小正方形网格的边长为
的大致图象(注:图中小正方形网格的边长为![]() ),根据图象填空:
),根据图象填空:
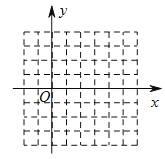
(![]() )当
)当![]() __________时,
__________时,![]() 有最__________值
有最__________值![]() __________.
__________.
(![]() )
)![]() 随
随![]() 的增大而减小的自变量
的增大而减小的自变量![]() 的取值范围是__________.
的取值范围是__________.
(![]() )结合图象直接写出
)结合图象直接写出![]() 时
时![]() 的范围:__________.
的范围:__________.
(![]() )结合图象直接写出
)结合图象直接写出![]() 时
时![]() 的取值范围:__________.
的取值范围:__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com