【题目】如图，已知点
，
，
，
的坐标分别为
，
，
，
．线段
，
，
组成的图形为图形
，点
沿
移动，设点移动的距离为
，直线
过点，且在点移动过程中，直线
随运动而运动．
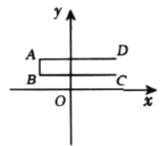
（1）若点过点时，求直线的解析式；
（2）当过点时，求值；
（3）①若直线与图形有一个交点，直接写出
的取值范围；
②若直线与图形有两个交点，直接写出的取值范围．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】某校组织一项公益知识竞赛，比赛规定：每个代表队由3名男生、4名女生和1名指导老师组成．但参赛时，每个代表队只能有3名队员上场参赛，指导老师必须参加，另外2名队员分别在3名男生和4名女生中各随机抽出一名．七年级（1）班代表队有甲、乙、丙三名男生和A、B、C、D4名女生及1名指导老师组成．求：
（1）抽到D上场参赛的概率；
（2）恰好抽到由男生丙、女生C和这位指导老师一起上场参赛的概率．（请用“画树状图”或“列表”的方式给出分析过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（2，2），B（4,0），C（4，-4）.
（1）请在图中画出△ABC向左平移6个单位长度后得到的△A1B1C1；
（2）以点O为位似中心，将△ABC缩小为原来的
，得到△A2B2C2，请在图中y轴右侧画出△A2B2C2,；
（3）填空：△AA1A2的面积为________________.
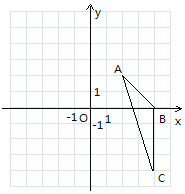
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】三辆汽车经过某收费站下高速时，在2个收费通道A，B中，可随机选择其中的一个通过．
（1）三辆汽车经过此收费站时，都选择A通道通过的概率是 ；
（2）求三辆汽车经过此收费站时，至少有两辆汽车选择B通道通过的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着技术的发展进步，某公司2018年采用的新型原料生产产品．这种新型原料的用量y（吨）与月份x之间的关系如图1所示，每吨新型原料所生产的产品的售价z（万元）与月份x之间的关系如图2所示．已知将每吨这种新型原料加工成的产品的成本为20万元．
（1）求出该公司这种新型原料的用量y（吨）与月份x之间的函数关系式；
（2）若该公司利用新型原料所生产的产品当月都全部销售，求哪个月利润最大，最大利润是多少？
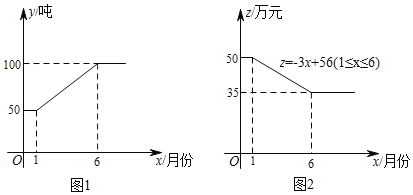
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y＝ax2+bx+c的图象如图，对称轴是直线x＝﹣1，有以下结论：①abc＞0；②4ac＜b2；③2a﹣b＝0；④a﹣b+c＞0；⑤9a﹣3b+c＞0．其中正确的结论有_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C＝90°，BC＝2
，AC＝2，点D是BC的中点，点E是边AB上一动点，沿DE所在直线把△BDE翻折到△B′DE的位置，B′D交AB于点F．若△AB′F为直角三角形，则AE的长为_____．
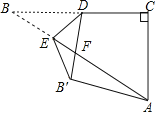
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（发现问题）爱好数学的小明在做作业时碰到这样的一道题目：
如图①，点O为坐标原点，⊙O的半径为1，点A（2，0）．动点B在⊙O上，连结AB，作等边△ABC（A，B，C为顺时针顺序），求OC的最大值
（解决问题）小明经过多次的尝试与探索，终于得到解题思路：在图①中，连接OB，以OB为边在OB的左侧作等边三角形BOE，连接AE．
（1）请你找出图中与OC相等的线段，并说明理由；
（2）求线段OC的最大值．
（灵活运用）
（3）如图②，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA＝2，PM＝PB，∠BPM＝90°，求线段AM长的最大值及此时点P的坐标．
（迁移拓展）
（4）如图③，BC＝4
，点D是以BC为直径的半圆上不同于B、C的一个动点，以BD为边作等边△ABD，请直接写出AC的最值．
查看答案和解析>>
科目：初中数学 来源： 题型：
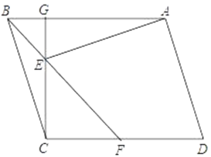
【题目】如图，在ABCD中，CG⊥AB于点G，∠ABF＝45°，F在CD上，BF交CG于点E，连接AE，且AE⊥AD．
（1）若BG＝2，BC＝
，求EF的长度；
（2）求证：CE+
BE＝AB．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
