【题目】如图，∠A+∠B+∠C+∠D+∠E+∠F=_______度.
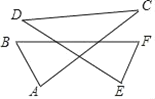
【答案】360°
【解析】
先根据图形的特点，将∠A +∠B、∠C +∠D和∠E +∠F分别转化成和它不相邻的外角，再根据邻补角的定义转化为一个三角形的内角，然后利用三角形的内角和定理求解即可.
如图，记BF交DE于G，交AC于H，DE交AC于I ，
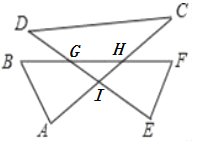
∵∠FHI＝∠A +∠B，
∴∠GHI＝180°-∠FHI＝180°-（∠A+ ∠B），
∵∠AIG＝∠C +∠D，
∴∠GIH＝180°-∠AIG＝180°-（∠C +∠D），
∵∠BGI＝∠E +∠F，
∴∠HGI＝180°-∠BGI＝180°-（∠E +∠F），
∵∠GHI+∠GIH +∠HGI＝180°，
∴180°-（∠A +∠B）+ 180°-（∠C +∠D）+ 180°-（∠E+ ∠F）＝180°，
∴∠A+∠B+∠C+∠D+∠E+∠F＝360°.
阳光试卷单元测试卷系列答案科目：初中数学 来源： 题型：
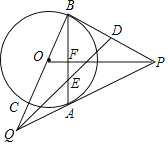
【题目】如图，P是⊙O外的一点，PA、PB是⊙O的两条切线，A、B是切点，PO交AB于点F，延长BO交⊙O于点C，交PA的延长交于点Q，连结AC．
（1）求证：AC∥PO；
（2）设D为PB的中点，QD交AB于点E，若⊙O的半径为3，CQ=2，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y=
的图象相交于点A（m，3）、B（﹣6，n），与x轴交于点C．
（1）求一次函数y=kx+b的关系式；
（2）结合图象，直接写出满足kx+b＞
的x的取值范围；
（3）若点P在x轴上，且S△ACP=
S△BOC，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在每个小正方形的边长为1的网格中，点A、B、C均在格点上，在△ABC的内部有一点P，满足S△PAB：S△PBC：S△PCA=1：2：3，请在如图所示的网格中，用无刻度直尺画出点P（保留画图痕迹）
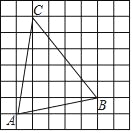
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程（组）或不等式（组）解应用题：
（1）甲工人接到240个零件的任务，工作1小时后，因要提前完成任务，调来乙和甲合作，合做了5小时完成.已知甲每小时比乙少做4个，那么甲、乙每小时各做多少个？
（2）某工厂准备购进
、
两种机器共20台用于生产零件，经调查2台型机器和1台型机器价格为18万元，1台型机器和2台型机器价格为21万元.
①求一台型机器和一台型机器价格分别是多少万元？
②已知1台型机器每月可加工零件400个，1台型机器每月可加工零件800个，经预算购买两种机器的价格不超过140万元，每月两种机器加工零件总数不低于12400个，那么有哪几种购买方案，哪种方案最省钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把下列各数﹣5，|﹣1.5|，﹣
，0，3
，﹣（﹣1）表示的点．
（1）画在数轴上；
（2）用“＜”把这些数连接起来；
（3）指出：负数是 ；分数是 ；非负整数是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
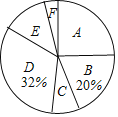
【题目】某校为了解学生最喜欢的球类运动情况，随机选取该校部分学生进行调查，要求每名学生只写一类最喜欢的球类运动．以下是根据调查结果绘制的统计图表的一部分．
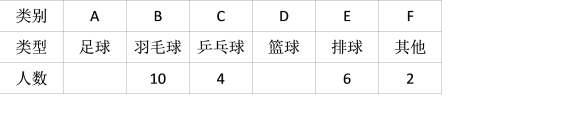
根据以上信息，解答下列问题：
（1）被调查的学生中，最喜欢乒乓球的有 人，最喜欢篮球的学生数占被调查总人数的百分比为 %；
（2）被调查学生的总数为 人，其中，最喜欢篮球的有 人，最喜欢足球的学生数占被调查总人数的百分比为 %；
（3）该校共有450名学生，根据调查结果，估计该校最喜欢排球的学生数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．
（1）求证：△ADE∽△ABC；
（2）若AD=3，AB=5，求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
