
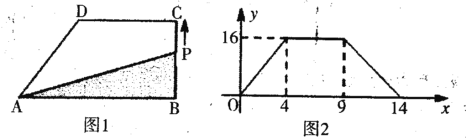
【题目】如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)当点P运动的路程x=4时,△ABP的面积为y= ;
(2)求:线段AB的长;
(3)求:梯形ABCD的面积是多少?
科目:初中数学 来源: 题型:
【题目】用“※”定义一种新运算:对于任意有理数a和b,规定a※b=ab2+2ab+a.
如:1※2=1×22+2×1×2+1=9
(1)(﹣2)※3= ;
(2)若![]() ※3=16,求a的值;
※3=16,求a的值;
(3)若2※x=m,(![]() x)※3=n(其中x为有理数),试比较m,n的大小.
x)※3=n(其中x为有理数),试比较m,n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由一些大小相同且棱长为1的小正方体组合成的简单几何体.
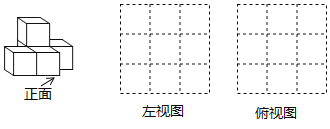
(1)该几何体的立体图如图所示,请在下面方格纸中分别画出它的左视图和俯视图(请涂上阴影):
(2)这个简单几何体的表面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,人们有吃粽子的习惯.某校数学兴趣小组为了了解本校学生喜爱粽子的情况,随机抽取了50名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图(注:每一位同学在任何一种分类统计中只有一种选择)
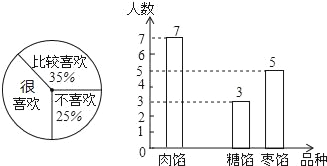
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”所对应的圆心角为 度;条形统计图中,喜欢“糖馅”粽子的人数为 人;
(2)若该校学生人数为800人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”粽子的人数之和;
(3)小军最爱吃肉馅粽子,小丽最爱吃糖馅粽子.某天小霞带了重量、外包装完全一样的肉馅、糖馅、枣馅、海鲜馅四种粽子各一只,让小军、小丽每人各选一只.请用树状图或列表法求小军、小丽两人中有且只有一人选中自己最爱吃的粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
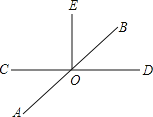
【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣40|+(b+8)2=0.点O是数轴原点.
![]()
(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园,诵读经典”活动,随机抽查了部分学生,对他们每天的课外阅读时长进行统计,并将结果分为四类:设每天阅读时长为t分钟,当0<t≤20时记为A类,当20<t≤40时记为B类,当40<t≤60时记为C类,当t>60时记为D类,收集的数据绘制成如下两幅不完整的统计图,请根据图中提供的信息,解答下列问题:

(1)这次共抽取了 名学生进行调查统计,扇形统计图中的D类所对应的扇形圆心角为 °;
(2)将条形统计图补充完整;
(3)若该校共有2000名学生,请估计该校每天阅读时长超过40分钟的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com