
����Ŀ���ҹ��߷��ֽӵ��鱨����������һ���ɴ�ֻA����������ʻ���߷���Ѹ���ɳ���ͧB�ϣ���ͼ1����ͼ2��l1��l2�ֱ��ʾ���������ں����ľ���s���������ʱ��t���֣�֮��Ĺ�ϵ������ͼ���ʴ����⣺
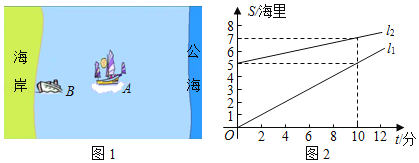
��1����ֱ��l1��ֱ��l2���� ����ʾB�������ľ�������ʱ��֮��Ĺ�ϵ
��A��B�Ƚϣ��� ���ٶȿ죻
�����һֱ��ȥ����ôB�� �������ܻ��ܣ���A��
�ܿ��ɴ�ֻA�ٶ����� ������/�֣���ͧB���ٶ����� ������/��
��2��l1��l2��Ӧ������һ�κ�������ʽS1��k1t+b1��S2��k2t+b2�У�k1��k2��ʵ���������ʲô����ֱ��д�������������ʽ
��3��15������B�ܷ���A��Ϊʲô��
��4����A���뺣��12����Ĺ���ʱ��B����������м�飬�մ��ٶȣ�B�ܷ���A���빫��ǰ�������أ�Ϊʲô��
���𰸡���1����ֱ��l1����B�����ܣ���0.2��0.5����2��k1��k2��ʵ�������Ƿֱ��ʾ��ͧB���ٶȺͿ��ɴ�ֻ���ٶȣ�S1��0.5t��S2��0.2t+5����3��15������B������A������������4��B����A���빫��ǰ�������أ�������
��������
��1�������������ͼ�Σ����Եõ�����ֱ�߱�ʾB�������ľ�������ʱ��֮��Ĺ�ϵ��
������ͼ2��֪��˭���ٶȿ죻
������ͼ�κ����⣬���Եõ�B�ܷ���A��
������ͼ2�е����ݿ��Լ�������ɴ�ֻA�Ϳ�ͧB���ٶȣ�
��2�����ݣ�1���еĽ�������⣬���Եõ�k1��k2��ʵ�����壬ֱ��д�����������ı���ʽ��
��3����t��15����ֱ����S1��S2�У�Ȼ��Ƚϴ�С���ɽ���⣻
��4����12����S2�����t��ֵ���ٽ����t��ֵ����S1�У�Ȼ����12�Ƚϴ�С���ɽ���⣮
�⣺��1��������֪�ɵã�
ֱ��l1��ʾB�������ľ�������ʱ��֮��Ĺ�ϵ��
�ʴ�Ϊ��ֱ��l1��
����ͼ�ɵã�
A��B�Ƚϣ�B���ٶȿ죬
�ʴ�Ϊ��B��
�����һֱ��ȥ����ôB����A��
�ʴ�Ϊ���ܣ�
�����ɴ�ֻA�ٶ��ǣ���7��5����10��0.2����/�֣���ͧB���ٶ��ǣ�5��10��0.5����/�֣�
�ʴ�Ϊ��0.2��0.5��
��2��������ɵã�
k1��k2��ʵ�������Ƿֱ��ʾ��ͧB���ٶȺͿ��ɴ�ֻ���ٶȣ�
S1��0.5t��S2��0.2t+5��
��3��15������B������A��
���ɣ���t��15ʱ��S2��0.2��15+5��8��S1��0.5��15��7.5��
��8��7.5��
��15������B������A��
��4��B����A���빫��ǰ�������أ�
���ɣ���S2��12ʱ��12��0.2t+5����t��35��
��t��35ʱ��S1��0.5��35��17.5��
��17.5��12��
��B����A���빫��ǰ�������أ�


 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĸ�С�������ֱ����2��3��4��6�ĸ����֣����ǵIJ��ʡ���״����С��ȫ��ͬ�������������һ��С���������Ϊx���ٴ�ʣ�µ����������������һ�����������Ϊy����A������Ϊ��x,y).���û���״ͼ���б��ķ�����д��A�����п��ܵ����꣬�������A�ڷ���������![]() ͼ���ϵĸ���.
ͼ���ϵĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
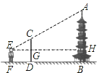
����Ŀ����ͼ��С��������һ�������ĸ߶ȣ����ó�һ�������ֱ���ڵ����ϣ�Ȼ���Լ��˺�ʹ�۾�ͨ����˵Ķ��˸պÿ�����������С���۾������![]() ����˶��������
����˶��������![]() ��С������˵ľ���
��С������˵ľ���![]() ����˵����ľ���
����˵����ľ���![]() �������������ĸ߶ȣ�
�������������ĸ߶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
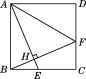
����Ŀ����ͼ��������ABCD�У�E��BC�ϵ�һ�㣬����AE����B����BH��AE������Ϊ��H���ӳ�BH��CD�ڵ�F������AF.
��1����֤AE��BF��
��2���������εı߳���5��BE��2����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijУ��Ǩ����Ҫ���ӽ�ʦ��ѧ�����������������������࣬�ֱ�Ϊ���˼䣨��һ����ס�ޣ���˫�˼䣨��������ס�ޣ������˼䣨���ĸ���ס�ޣ�����ʵ����Ҫ�����˼��������20��30֮�䣨����20��30���������˼��������˫�˼��5����
��1����2018��ѧУ������Ϊ64�����Ժ��������ӣ�Ԥ��2020���������ﵽ121������2018��2020��������������ƽ�������ʣ�
��2�������ͬ�����ҵ�����Ϊ121���������ɹ�����ʦ��ס�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
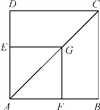
����Ŀ����ͼ��G��������ABCD�Խ���AC��һ�㣬��GE��AD��GF��AB������ֱ�Ϊ��E��F.
��֤���ı���AFGE���ı���ABCD���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ӿ���![]() ��
��![]() ǧ��
ǧ��![]() �г���ȥ
�г���ȥ![]() �У��Ҵ�ͬһ·���ϵ�
�У��Ҵ�ͬһ·���ϵ�![]() �г���Ҳȥ��
�г���Ҳȥ��![]() �У�������
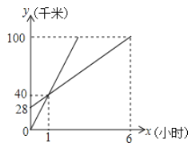
�У�������![]() �еľ�������ʻʱ��ĺ�����ϵ��ͼ��ʾ��
�еľ�������ʻʱ��ĺ�����ϵ��ͼ��ʾ��![]() �������룬
�������룬![]() ����ʱ�䣩��
����ʱ�䣩��
��1��![]() ����
����![]() �еľ����� ǧ�ף�
�еľ����� ǧ�ף�
��2�����ٶ��� ǧ��/ʱ���ҵ��ٶ��� ǧ��/ʱ��
��3���ױ����缸Сʱ����![]() �У�
�У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
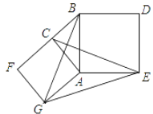
����Ŀ����ͼ���ֱ���![]() ��ֱ�DZ�
��ֱ�DZ�![]() ��б��
��б��![]() Ϊ��������������
��������������![]() ��������
��������![]() ������
������![]() ��
��![]() ��
��![]() ���������н��ۣ�
���������н��ۣ�
��![]() ��
��
��![]()
��![]()
��![]() ������ȷ���ǣ� ��
������ȷ���ǣ� ��
A.�ڢۢ�B.�٢ڢ�C.�٢ڢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com