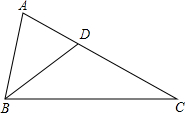
如图.已知BD是∠ABC的角平分线.且∠C=∠DBC.∠BDA=72°.求△ABC各内角度数．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

6．

如图，已知BD是∠ABC的角平分线，且∠C=∠DBC，∠BDA=72°，求△ABC各内角度数．

分析由∠C=∠DBC、∠BDA=72°结合三角形外角的性质，即可得出∠C=∠DBC=36°，由BD是∠ABC的角平分线可求出∠ABC=2∠DBC=72°，再利用三角形内角和定理即可求出∠A的度数．

解答解：∵∠C=∠DBC，∠BDA=∠C+∠DBC=72°，
∴∠C=∠DBC=36°．
∵BD是∠ABC的角平分线，
∴∠ABC=2∠DBC=72°，
∴∠A=180°-∠ABC-∠C=72°．

点评本题考查了三角形内角和定理、角平分线以及三角形外角的性质，牢记“三角形内角和是180°”是解题的关键．

练习册系列答案

天利38套高中名校期中期末联考测试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

7．生态文明贵阳国际论坛作为我国目前唯一以生态文明为主题的国家级国际性论坛，现已被纳入国家“一带一路”总体规划，持续四届的成功举办，已相继吸引近7000名各国政要及嘉宾出席，7000这个数用科学记数法可表示为（　　）

A．

70×10²

B．

7×10³

C．

0.7×10⁴

D．

7×10⁴

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

17．已知直线l₁：y=-$\frac{2}{3}$x+$\frac{2}{3}$a与直线l₂：y=$\frac{3}{2}$x-$\frac{a-1}{2}$的交点在第二象限，则a的取值范围是（　　）

A．

-$\frac{1}{2}$＜a＜$\frac{3}{7}$

B．

a＞-$\frac{1}{2}$

C．

a$＜\frac{3}{7}$

D．

-$\frac{1}{2}$≤a≤$\frac{3}{7}$

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

14．

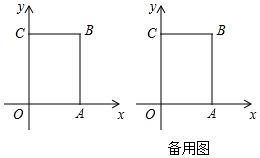如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a，b满足|a-4|+$\sqrt{b-6}$=0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动．
（1）点B的坐标为（4，6），当点P移动3.5秒时，点P的坐标（1，2）；
（2）在移动过程中，当点P到x轴的距离为4个单位长度时，求点P移动的时间；
（3）在移动过程中，当△OBP的面积是10时，求点P移动的时间．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．若正比例函数y=-2x的图象与一次函数y=x+m的图象交于点A，且点A的横坐标为-3．
（1）求该一次函数的解析式；
（2）直接写出方程组$\left\{\begin{array}{l}{y=-2x}\\{y=x+m}\end{array}\right.$的解．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

11．

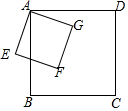如图，正方形ABCD的边长为2cm，正方形AEFG的边长为1cm，正方形AEFG绕点A旋转的过程中，线段CF的长的最小值为$\sqrt{2}$cm．