
| A. | 有1对或2对 | B. | 只有1对 | C. | 只有2对 | D. | 有2对或3对 |
分析 根据“友好点”的定义知,函数y1图象上点A(a,-$\frac{1}{a}$)关于原点的对称点B(-a,$\frac{1}{a}$)一定位于直线y2上,即方程ka2-(k+1)a+1=0 有解,整理方程得(a-1)(ka-1)=0,据此可得答案.
解答 解:设A(a,-$\frac{1}{a}$),
由题意知,点A关于原点的对称点B(-a,$\frac{1}{a}$)在直线y2=kx+1+k上,
则$\frac{1}{a}$=-ak+1+k,
整理,得:ka2-(k+1)a+1=0 ①,
即(a-1)(ka-1)=0,
∴a-1=0或ka-1=0,
则a=1或ka-1=0,
若k=0,则a=1,此时方程①只有1个实数根,即两个函数图象上的“友好点”只有1对;
若k≠0,则a=1或a=$\frac{1}{k}$,此时方程①有2个实数根,即两个函数图象上的“友好点”有2对,
综上,这两个函数图象上的“友好点”对数情况为1对或2对,
故选:A.
点评 本题主要考查直线和双曲线上点的坐标特征及关于原点对称的点的坐标,将“友好点”的定义,根据关于原点对称的点的坐标特征转化为方程的问题求解是解题的关键.


科目:初中数学 来源: 题型:选择题
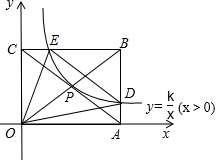 如图,矩形OABC的顶点A、C坐标分别是(8,0),(0,4),反比例函数y=$\frac{k}{x}$(x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( )
如图,矩形OABC的顶点A、C坐标分别是(8,0),(0,4),反比例函数y=$\frac{k}{x}$(x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( )| A. | 14 | B. | 12 | C. | 15 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
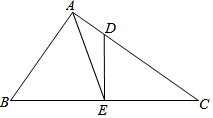 如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.
如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).| 分组/元 | 频 数 | 频 率 |
| 1000<x<1200 | 3 | 0.060 |
| 1200<x<1400 | 12 | 0.240 |
| 1400<x<1600 | 18 | 0.360 |
| 1600<x<1800 | a | 0.200 |
| 1800<x<2000 | 5 | b |
| 2000<x<2200 | 2 | 0.040 |
| 合计 | 50 | 1.000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
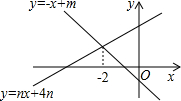 如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )
如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )| A. | -5 | B. | -4 | C. | -3 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.
学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
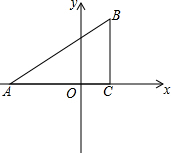 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=$\frac{3}{4}$AC
已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=$\frac{3}{4}$AC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com